Глава 7. Краевые задачи оптимального управления………………..226 2 страница
Определение 1. Оператор F(x) дифференцируем по Фреше в точке 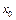 , если существует линейный ограниченный оператор
, если существует линейный ограниченный оператор 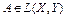 такой, что
такой, что
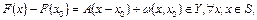 (1)
(1)
где 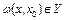 удовлетворяет условию
удовлетворяет условию
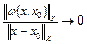 при
при 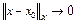 . (2)
. (2)
Оператор 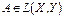 называется производной Фреше оператора F(x) в точке
называется производной Фреше оператора F(x) в точке 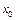 и обозначается
и обозначается 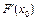 (либо
(либо 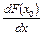 ). Здесь L(X,Y) – пространство линейных ограниченных операторов, действующих из X в Y, L(X,Y) – банахово пространство.
). Здесь L(X,Y) – пространство линейных ограниченных операторов, действующих из X в Y, L(X,Y) – банахово пространство.
Если ввести обозначение 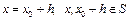 , то соотношения (1), (2) запишутся так:
, то соотношения (1), (2) запишутся так:
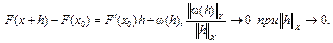 (3)
(3)
Определение 2. Если оператор F(x) дифференцируем по Фреше в точке 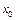 , то выражение
, то выражение 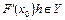 называется дифференциалом Фреше оператора F(x) в точке
называется дифференциалом Фреше оператора F(x) в точке 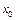 и обозначается
и обозначается 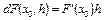 .
.
Иногда производную Фреше 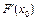 оператора F(x) в точке
оператора F(x) в точке 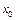 называют сильной производной, а дифференциал
называют сильной производной, а дифференциал 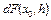 – сильным дифференциалом.
– сильным дифференциалом.
Основные свойства. 1. Из дифференцируемости по Фреше оператора F(x) в точке 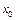 следует его непрерывность в точке
следует его непрерывность в точке 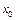 . В самом деле, если
. В самом деле, если 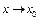 , то из (1) имеем
, то из (1) имеем 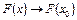 .
.
2. Если 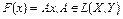 , то
, то 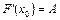 . Действительно, по определению имеем
. Действительно, по определению имеем 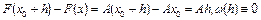 . В частности, если
. В частности, если  , то
, то 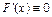 , т.е.
, т.е. 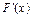 – нулевой оператор.
– нулевой оператор.
3. Если операторы 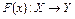 и
и 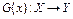 дифференцируемы по Фреше в точке
дифференцируемы по Фреше в точке 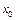 , то оператор
, то оператор 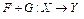 дифференцируем по Фреше в точке
дифференцируем по Фреше в точке 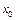 , причем
, причем 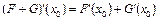 . Действительно,
. Действительно, 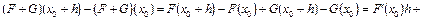
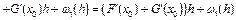 , где
, где 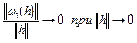 .
.
Аналогичным путем можно доказать, что 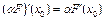 , где
, где 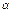 – скаляр.
– скаляр.
4. Пусть X, Y, Z – банаховы пространства, операторы  . Существуют производные
. Существуют производные 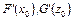 , причем
, причем 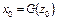 . Следовательно, оператор F(x) непрерывен в точке
. Следовательно, оператор F(x) непрерывен в точке 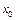 , оператор G(z) непрерывен в точке
, оператор G(z) непрерывен в точке 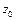 . Тогда определена и непрерывна в точке
. Тогда определена и непрерывна в точке 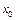 суперпозиция операторов
суперпозиция операторов 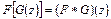 .
.
Покажем, что суперпозиция операторов 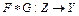 дифференцируема по Фреше в точке
дифференцируема по Фреше в точке 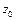 , причем
, причем 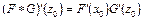 . В самом деле, имеем
. В самом деле, имеем 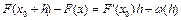 ,
,  где
где 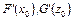 – линейные ограниченные операторы,
– линейные ограниченные операторы, 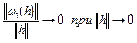 ,
, 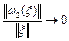 при
при 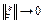 .
.
Тогда
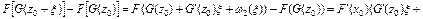
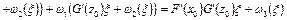 ,
,
где 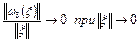 . Отсюда следует, что
. Отсюда следует, что 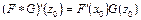 .
.
Дифференциал Гато. Пусть оператор 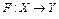 , X, Y – банаховы пространства.
, X, Y – банаховы пространства.
Определение 3. Пусть оператор F(x) определен в S–окрестности точки 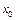 . Дифференциалом Гато (или слабым дифференциалом) оператора F(x) в точке
. Дифференциалом Гато (или слабым дифференциалом) оператора F(x) в точке 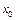 называется предел
называется предел
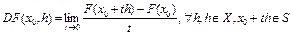 .
.
Иногда выражение 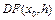 называется первой вариацией оператора F(x) в точке
называется первой вариацией оператора F(x) в точке 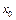 . В общем случае, при фиксированном
. В общем случае, при фиксированном 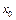 оператор
оператор 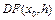 является нелинейным.
является нелинейным.
Определение 4. Если 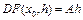 , где A – линейный ограниченный оператор, (т.е.
, где A – линейный ограниченный оператор, (т.е.  ), то оператор A называется производной Гато (или слабой производной) оператора F(x) в точке
), то оператор A называется производной Гато (или слабой производной) оператора F(x) в точке 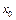 и обозначается
и обозначается 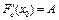 .
.
Заметим, что: 1. Если оператор F(x) дифференцируем по Фреше в точке 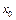 , то оператор F(x) дифференцируем по Гато в точке
, то оператор F(x) дифференцируем по Гато в точке 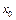 и эти производные совпадают, т.е.
и эти производные совпадают, т.е. 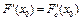 . Действительно, из дифференцируемости по Фреше имеем
. Действительно, из дифференцируемости по Фреше имеем
 ,
, 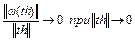 .
.
С другой стороны, предел
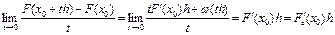 .
.
Отсюда следует, что 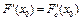 .
.
2. Из дифференцируемости оператора F(x) по Гато не следует его дифференцируемость по Фреше.
Формула конечных приращений Лагранжа. Оператор F(x) непрерывно дифференцируем в точке 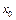 по Фреше, если он дифференцируем в S–окрестности точки
по Фреше, если он дифференцируем в S–окрестности точки 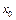 и оператор
и оператор 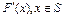 непрерывен в точке
непрерывен в точке 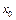 .
.
Теорема 1. Пусть оператор F(x) непрерывно дифференцируем в S окрестности точки 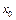 . Тогда справедлива формула
. Тогда справедлива формула
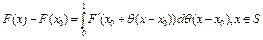 . (4)
. (4)
Доказательство. Если оператор  ,
, 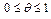 , то
, то 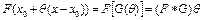 . Производная по Фреше
. Производная по Фреше 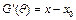 . Тогда производная
. Тогда производная 
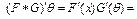
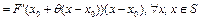 . Интегрируя данное тождество по
. Интегрируя данное тождество по 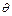 в пределах от 0 до 1, получим
в пределах от 0 до 1, получим
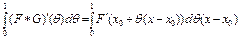 .
.
Отсюда с учетом того, что
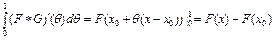 ,
,
получим формулу (4). Теорема доказана.
Условие Липшица. Пусть оператор F(x) определен на некотором множестве  банахова пространства X,
банахова пространства X, 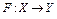 , Y – банахово пространство.
, Y – банахово пространство.
Определение 4. Говорят, что оператор F(x) удовлетворяет на множестве 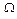 условию Липшица, если
условию Липшица, если
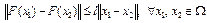 , (5)
, (5)
где 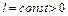 – постоянная Липшица.
– постоянная Липшица.
Лемма 1. Если оператор F(x) непрерывно дифференцируем по Фреше на выпуклом множестве 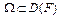 , причем
, причем 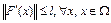 , то оператор F(x) удовлетворяет условию Липшица на
, то оператор F(x) удовлетворяет условию Липшица на 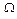 , т.е.
, т.е.
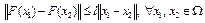 .
.
Доказательство. Согласно формуле конечных приращений Лагранжа (4) имеем
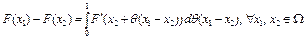 ,
,
где 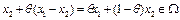 в силу выпуклости множества
в силу выпуклости множества  . Отсюда имеем
. Отсюда имеем

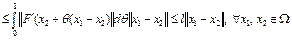 .
.
Лемма доказана.
Лемма 2. Пусть оператор F(x) непрерывно дифференцируем по Фреше на выпуклом множестве  и
и 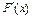 удовлетворяет на
удовлетворяет на  условию Липшица, т.е.
условию Липшица, т.е.
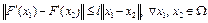 . (6)
. (6)
Тогда верна оценка
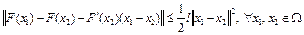 . (7)
. (7)
Доказательство. Согласно формуле конечных приращений Лагранжа (4), имеем
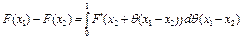 .
.
Тогда
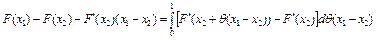 .
.
Отсюда следует, что
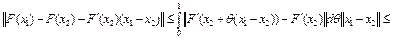
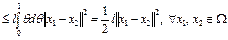 .
.
Лемма доказана.
Дифференцирование нелинейных функционалов. Пусть 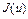 нелинейный функционал, определенный на некотором множестве U банахова пространства X со значениями в банаховом пространстве
нелинейный функционал, определенный на некотором множестве U банахова пространства X со значениями в банаховом пространстве 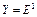 , где
, где 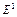 – вещественная ось. Поскольку
– вещественная ось. Поскольку 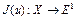 , где
, где 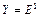 , то остаются верными все вышеприведенные результаты.
, то остаются верными все вышеприведенные результаты.
Определение 5. Пусть X – банахово пространство и пусть функционал 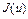 определен в окрестности
определен в окрестности 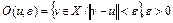 точки u. Говорят, что функционал J(u) дифференцируем по Фреше в точке u, если существует линейный ограниченный функционал
точки u. Говорят, что функционал J(u) дифференцируем по Фреше в точке u, если существует линейный ограниченный функционал 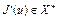 такой, что
такой, что
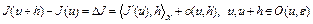 , (8)
, (8)
где число  удовлетворяет условию
удовлетворяет условию
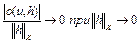 . (9)
. (9)
Здесь 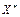 – сопряженное пространство, оно содержит все линейные ограниченные функционалы, определенные на банаховом пространстве X, пространство
– сопряженное пространство, оно содержит все линейные ограниченные функционалы, определенные на банаховом пространстве X, пространство 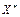 – банахово.
– банахово.
Определение 6. Величина 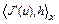 называется дифференциалом Фреше функционала
называется дифференциалом Фреше функционала 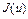 в точке u, обозначается
в точке u, обозначается  . Дифференциал Фреше
. Дифференциал Фреше 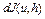 является главной линейной частью приращения функционала.
является главной линейной частью приращения функционала.
Иногда элемент 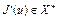 называется градиентом (по Фреше) функционала
называется градиентом (по Фреше) функционала 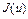 в точке u.
в точке u.
Заметим, что: 1. Если функционалы J(u), G(u) дифференцируемы по Фреше в точке u, то функционал 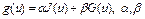 – числа, дифференцируем по Фреше, причем
– числа, дифференцируем по Фреше, причем 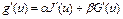 ;
;
2. Пусть функционал 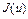 дифференцируем по Фреше в точке
дифференцируем по Фреше в точке 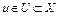 , а функция
, а функция 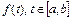 от одной переменной дифференцируема в точке
от одной переменной дифференцируема в точке 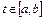 , где
, где 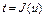 , тогда функционал
, тогда функционал 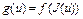 дифференцируем по Фреше в точке u, причем
дифференцируем по Фреше в точке u, причем  .
.
Определение 7. Говорят, что функционал 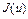 непрерывно дифференцируем по Фреше на множестве U из банахова пространства X, если он дифференцируем по Фреше во всех точках
непрерывно дифференцируем по Фреше на множестве U из банахова пространства X, если он дифференцируем по Фреше во всех точках 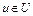 и
и 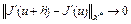 при
при 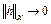 для всех
для всех 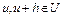 . Множество всех функционалов, непрерывно дифференцируемых на U, обозначим через
. Множество всех функционалов, непрерывно дифференцируемых на U, обозначим через 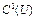 .
.
Теорема 2. Пусть функционал J(u) непрерывно дифференцируем по Фреше в 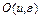 окрестности точки u. Тогда справедлива формула конечных приращений Лагранжа
окрестности точки u. Тогда справедлива формула конечных приращений Лагранжа
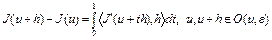 .
.
Доказательство теоремы следует из теоремы 1.
Определение 8. Говорят, что функционал 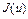 удовлетворяет на множестве
удовлетворяет на множестве 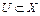 условию Липшица, если
условию Липшица, если
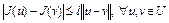 ,
,
где 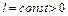 – постоянная Липшица.
– постоянная Липшица.
Лемма 3. Если функционал J(u) непрерывно дифференцируем по Фреше на выпуклом множестве 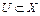 , причем
, причем 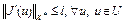 , то функционал
, то функционал 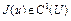 удовлетворяет условию Липшица на множестве U.
удовлетворяет условию Липшица на множестве U.
Доказательство леммы следует из леммы 1.
Определение 9. Пусть функционал 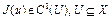 . Говорят, что градиент
. Говорят, что градиент 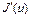 удовлетворяет условию Липшица на множестве U, если
удовлетворяет условию Липшица на множестве U, если
 ,
,
где 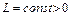 – постоянная Липшица. Множество таких функционалов обозначим через
– постоянная Липшица. Множество таких функционалов обозначим через 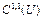 .
.
Лемма 4. Пусть U – выпуклое множество банахова пространства X, функционал 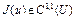 . Тогда верна оценка
. Тогда верна оценка
 .
.
Доказательство леммы следует из леммы 2.
Определение 10. Пусть функционал 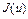 определен в
определен в 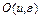 окрестности точки u. Дифференциалом Гато (или слабым дифференциалом) функционала
окрестности точки u. Дифференциалом Гато (или слабым дифференциалом) функционала 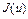 в точке u называется предел
в точке u называется предел
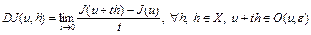 .
.
В том случае, когда 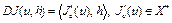 , функционал
, функционал 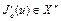 называют производной Гато (или слабой производной) функционала
называют производной Гато (или слабой производной) функционала 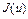 в точке u.
в точке u.
Пример 1. Пусть H – гильбертово пространство. Функционал 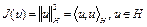 . Функционал
. Функционал 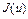 дифференцируем по Фреше в любой точке
дифференцируем по Фреше в любой точке 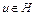 . В самом деле, (см. (8), (9))
. В самом деле, (см. (8), (9))
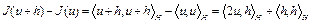 ,
,
где 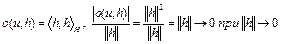 . Отсюда следует, что
. Отсюда следует, что 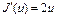 , функционал
, функционал 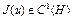 .
.
Пример 2. Рассмотрим функционал
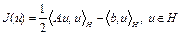 ,
,
где оператор  . Покажем, что функционал
. Покажем, что функционал 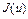 дифференцируем по Фреше в каждой точке
дифференцируем по Фреше в каждой точке 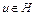 . Действительно,
. Действительно,
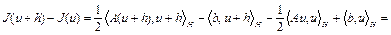
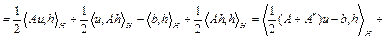
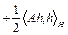 ,
,
где  – оператор, сопряженный к оператору A,
– оператор, сопряженный к оператору A, 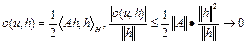 при
при 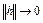 . Тогда
. Тогда 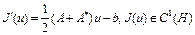 . В случае
. В случае 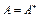 , A – самосопряженный оператор,
, A – самосопряженный оператор, 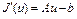 .
.
Рекомендуемая литература: Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. – М.: Наука, 1989.
ЛЕКЦИЯ 3.ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Изложены теоремы существования и единственности решения задачи Коши для дифференциального уравнения в банаховом пространстве.
Принцип сжимающих отображений. Пусть Ф(x)– нелинейный оператор с областью определения 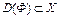 и с областью значений
и с областью значений  , X – банахово пространство. Пусть пересечение
, X – банахово пространство. Пусть пересечение 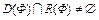 , где
, где 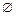 – пустое множество.
– пустое множество.
Определение 1. Пусть оператор Ф(x) определен на множестве 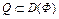 . Оператор Ф(x),
. Оператор Ф(x), 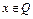 называется сжимающим оператором на множестве Q банахова пространства X, если существует число
называется сжимающим оператором на множестве Q банахова пространства X, если существует число 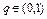 такое, что
такое, что
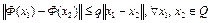 .
.
Теорема 1. Пусть оператор Ф(x) определен в замкнутом множестве Q банахова пространства X, отображает Q в себя и является на Q сжимающим оператором с коэффициентом сжатия 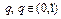 . Тогда:
. Тогда:
1) оператор Ф(x) , 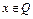 имеет единственную неподвижную точку
имеет единственную неподвижную точку 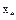 на Q;
на Q;
2) последовательность 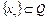 , где
, где  , с любой начальной точкой
, с любой начальной точкой  , сильно сходится к точке
, сильно сходится к точке  , т.е.
, т.е.  ;
;
3) справедлива следующая оценка скорости сходимости
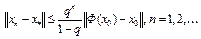 . (1)
. (1)
Доказательство. Так как оператор Ф(x) отображает Q в себя, то верно включение 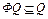 . Следовательно, последовательность
. Следовательно, последовательность 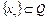 , где
, где 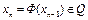 . Обозначим через
. Обозначим через 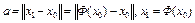 . Отметим, что
. Отметим, что
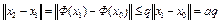 ,
,
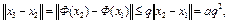
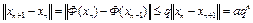 .
.
а) покажем, что 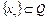 – фундаментальная последовательность. В самом деле, для любого фиксированного числа p имеем
– фундаментальная последовательность. В самом деле, для любого фиксированного числа p имеем
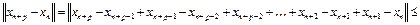
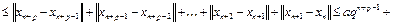
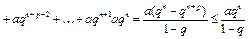 ,
,
как сумма убывающей геометрической прогрессии. Отсюда следует, что
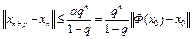 . (2)
. (2)
Следовательно, последовательность 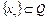 является фундаментальной, т.е. для любого
является фундаментальной, т.е. для любого 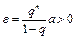 существует номер
существует номер  такой, что при всех
такой, что при всех 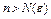 и любого натурального числа p выполняется неравенство
и любого натурального числа p выполняется неравенство 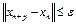 .
.
б) так как X банахово пространство, 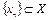 , то последовательность
, то последовательность 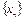 сходится к некоторой точке
сходится к некоторой точке 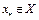 . Поскольку
. Поскольку 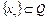 , Q – замкнутое множество, то
, Q – замкнутое множество, то 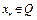 .
.
в) докажем, что 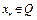 является неподвижной точкой оператора Ф(x), т.е.
является неподвижной точкой оператора Ф(x), т.е. 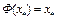 . По условию теоремы оператор
. По условию теоремы оператор 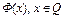 является сжимающим на Q. Из определения сжимающего оператора следует, что если
является сжимающим на Q. Из определения сжимающего оператора следует, что если 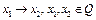 , то
, то 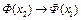 . Следовательно, оператор Ф(x) является непрерывным на Q. Тогда из
. Следовательно, оператор Ф(x) является непрерывным на Q. Тогда из 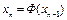 при
при 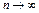 следует, что
следует, что 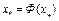 , где
, где 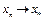 при
при 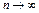 , оператор Ф(x) непрерывен.
, оператор Ф(x) непрерывен.
г) докажем, что 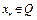 – единственная неподвижная точка оператора Ф(x) на Q. Предположим противное, т.е. имеется другая неподвижная точка
– единственная неподвижная точка оператора Ф(x) на Q. Предположим противное, т.е. имеется другая неподвижная точка 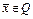 . Тогда имеем
. Тогда имеем 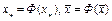 . Разность
. Разность  . Отсюда с учетом того, что оператор
. Отсюда с учетом того, что оператор 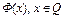 сжимающий, получим
сжимающий, получим 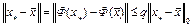 . Так как
. Так как 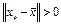 , то величина
, то величина 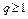 . Это противоречит тому, что
. Это противоречит тому, что 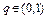 . Следовательно, данное неравенство возможно только при
. Следовательно, данное неравенство возможно только при 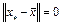 , т.е.
, т.е. 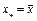 .
.
Дата добавления: 2015-08-21; просмотров: 1290;
