Глава 7. Краевые задачи оптимального управления………………..226 5 страница
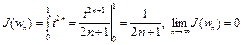 .
.
Отсюда следует, что последовательность 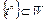 является минимизирующей. Однако предельная точка
является минимизирующей. Однако предельная точка 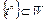 не является элементом множества W. С другой стороны, если
не является элементом множества W. С другой стороны, если 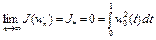 , где
, где 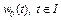 – предельная точка последовательности
– предельная точка последовательности 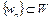 , то
, то 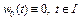 . Так как
. Так как 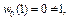 то
то 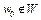 . Итак, значение нижней грани функционала
. Итак, значение нижней грани функционала  на множестве W равно нулю, т.е.
на множестве W равно нулю, т.е. 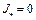 . Однако на множестве W нет элемента, где значение функционала равно нулю.
. Однако на множестве W нет элемента, где значение функционала равно нулю.
Для применения теоремы 2 необходимы легко проверяемые достаточные условия слабой бикомпактности множества W и слабой полунепрерывности снизу функционала  на множестве W банахова пространства X. Эти условия приведены в следующей главе.
на множестве W банахова пространства X. Эти условия приведены в следующей главе.
ГЛАВА 2.ВЫПУКЛЫЙ АНАЛИЗ В БАНАХОВОМ ПРОСТРАНСТВЕ
Приведены основные сведения из выпуклого анализа применительно к задачам оптимального управления: выпуклые множества и их свойства, выпуклые функционалы и их свойства; критерий выпуклости гладких функционалов, сильно выпуклые функционалы и их свойства; теорема о глобальном минимуме, условие оптимальности, проекция точки на множество; изложены основы теории отделимости выпуклых множеств, метода множителей Лагранжа, теоремы о существовании седловой точки; достаточные условия слабой бикомпактности выпуклых множеств и слабой полунепрерывности снизу выпуклых функционалов и достижение нижней грани функционала на множестве рефлексивного банахова пространства.
ЛЕКЦИЯ 6.ВЫПУКЛЫЕ МНОЖЕСТВА И ВЫПУКЛЫЕ ФУНКЦИОНАЛЫ
Выпуклые множества. Пусть X банахово пространство, U – некоторое множество из X.
Определение 1. Множество U называется выпуклым, если оно содержит вместе с любыми двумя своими точками u, v и отрезок  , соединяющий эти точки.
, соединяющий эти точки.
Определение 2. Множество 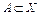 называется аффинным многообразием, если оно содержит вместе с любыми двумя своими точками u и v и прямую
называется аффинным многообразием, если оно содержит вместе с любыми двумя своими точками u и v и прямую 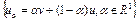 .
.
Определение 3. Множество 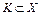 называется конусом (с вершиной в нуле), если оно содержит вместе с любой своей точкой v и весь луч
называется конусом (с вершиной в нуле), если оно содержит вместе с любой своей точкой v и весь луч 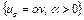 .
.
Пересечение любого числа выпуклых множеств является выпуклым. Конус K является выпуклым множеством тогда и только тогда, когда 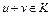 для любых
для любых 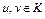 .
.
Аффинное множество A является линейным подпространством в X тогда и только тогда, когда оно содержит начало координат, т.е.  .
.
Определение 4.Пересечение всех выпуклых множеств, содержащих множество U, называется выпуклой оболочкой множества U и обозначается 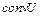 .
.
Аналогично вводятся понятия конической оболочки множества U, обозначается 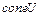 , аффинной оболочки множества U, обозначается
, аффинной оболочки множества U, обозначается 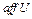 .
.
Определение 5. Пусть 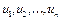 элементы банахова пространства. Элемент
элементы банахова пространства. Элемент  называется выпуклой комбинацией точек
называется выпуклой комбинацией точек 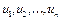 .
.
Аналогично: а) элемент 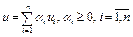 называется конической комбинацией точек
называется конической комбинацией точек 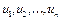 ; б) элемент
; б) элемент 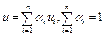 называется аффинной комбинацией точек
называется аффинной комбинацией точек 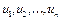 ; в) элемент
; в) элемент 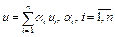 – любые числа, называется линейной комбинацией точек
– любые числа, называется линейной комбинацией точек 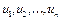 .
.
Теорема 1. Выпуклая оболочка множества U содержит все конечные выпуклые комбинации точек из U.
Доказательство. Пусть W – множество, содержащее все конечные выпуклые комбинации точек из U. Множество W – выпукло. В самом деле, если точки 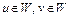 , то точки
, то точки 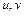 представимы в виде
представимы в виде
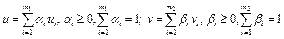 .
.
Тогда для любого 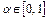 , имеем
, имеем
 ,
,
где 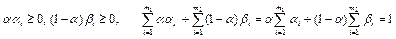 . Следовательно, элемент
. Следовательно, элемент 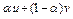 является выпуклой комбинацией точек
является выпуклой комбинацией точек 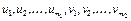 , поэтому
, поэтому 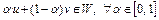 . Отсюда следует, что множество W выпукло. Заметим, что
. Отсюда следует, что множество W выпукло. Заметим, что 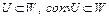 , где
, где 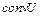 – пересечение всех выпуклых множеств, содержащих U. С другой стороны, каждая точка из W содержится в любом выпуклом множестве, содержащем U, и поэтому
– пересечение всех выпуклых множеств, содержащих U. С другой стороны, каждая точка из W содержится в любом выпуклом множестве, содержащем U, и поэтому 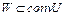 . Из
. Из 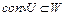 и
и 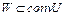 следует
следует 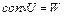 . Теорема доказана.
. Теорема доказана.
Аналогичным путем могут быть доказаны следующие утверждения: а) выпуклая коническая оболочка множества U содержит все выпуклые конические комбинации точек из U; б) выпуклая аффинная оболочка множества U содержит все выпуклые конечные аффинные комбинации точек из U.
Теорема 2. Множество U выпукло тогда и только тогда, когда оно совпадает со своей выпуклой оболочкой.
Доказательство. Покажем, что выпуклое множество U содержит все конечные выпуклые комбинации своих точек. Докажем это методом математической индукции. В самом деле, если 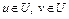 , то
, то 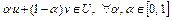 . Пусть для m точек
. Пусть для m точек 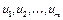 выпуклая комбинация этих точек
выпуклая комбинация этих точек 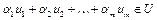 ,
, 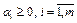 ,
, 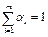 .
.
Докажем, что 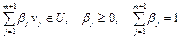 . Действительно,
. Действительно, 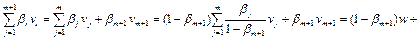
 , где
, где 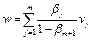 . Заметим, что
. Заметим, что 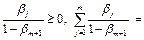
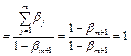 . Следовательно,
. Следовательно, 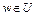 в силу того, что она является выпуклой комбинацией m точек из U. Тогда
в силу того, что она является выпуклой комбинацией m точек из U. Тогда 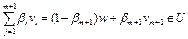 по определению выпуклого множества. Как следует из доказательства теоремы 1,
по определению выпуклого множества. Как следует из доказательства теоремы 1, 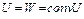 . Теорема доказана.
. Теорема доказана.
Аналогичным путем могут быть доказаны следующие утверждения:
а) множество U является выпуклым конусом тогда и только тогда, когда оно совпадает со своей конической оболочкой;
б) множество U является аффинным многообразием тогда и только тогда, когда оно совпадает со своей аффинной оболочкой.
Определение 6. Выпуклым многогранником называется выпуклая оболочка конечного множества точек.
Выпуклые функционалы. Пусть функционал  определен на множестве U банахова пространства X.
определен на множестве U банахова пространства X.
Определение 7. Функционал  , определенный на выпуклом множестве U банахова пространства X , называется выпуклым на U, если
, определенный на выпуклом множестве U банахова пространства X , называется выпуклым на U, если
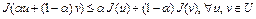 при всех
при всех 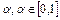 . (1)
. (1)
Если в (1) равенство возможно только при  и
и 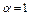 , то функционал J(u) строго выпуклый на U. Функционал
, то функционал J(u) строго выпуклый на U. Функционал 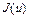 вогнутый (строго вогнутый) на U, если J(u) выпуклый (строго выпуклый).
вогнутый (строго вогнутый) на U, если J(u) выпуклый (строго выпуклый).
Определение 8. Функционал 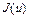 , определенный на выпуклом множестве U гильбертова пространства H, сильно выпуклый на U, если существует число
, определенный на выпуклом множестве U гильбертова пространства H, сильно выпуклый на U, если существует число 
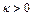 такое, что
такое, что
 ,
,
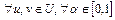 . (2)
. (2)
Величина 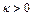 называется коэффициентом сильной выпуклости функционала
называется коэффициентом сильной выпуклости функционала  на множестве U.
на множестве U.
Теорема 3. Пусть  – выпуклое множество банахова пространства X. Для того, чтобы функционал
– выпуклое множество банахова пространства X. Для того, чтобы функционал  был выпуклым на U, необходимо и достаточно, чтобы выполнялось неравенство
был выпуклым на U, необходимо и достаточно, чтобы выполнялось неравенство
 . (3)
. (3)
Доказательство. Необходимость. Пусть 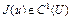 выпуклый функционал на выпуклом множестве U. Покажем, что выполнено неравенство (3). Так как
выпуклый функционал на выпуклом множестве U. Покажем, что выполнено неравенство (3). Так как
 ,
,
то
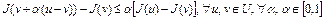 . (4)
. (4)
Согласно формуле конечных приращений Лагранжа, имеем (см. лекцию 2)
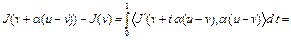
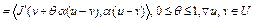 ,
,
где 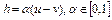 . Теперь неравенство (4) запишется так
. Теперь неравенство (4) запишется так
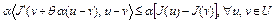 .
.
Отсюда после деления на 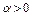 и при
и при 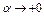 получаем неравенство (3). Необходимость доказана.
получаем неравенство (3). Необходимость доказана.
Достаточность. Пусть выполнено неравенство (3), где  – выпуклое множество. Покажем, что
– выпуклое множество. Покажем, что  выпуклый функционал на U. Из (3) имеем
выпуклый функционал на U. Из (3) имеем
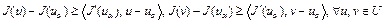 , (5) где
, (5) где  . Из (5) следует, что
. Из (5) следует, что
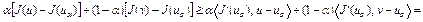
 .
.
Тогда 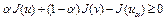 . Это означает, что функционал
. Это означает, что функционал  выпуклый на множестве U. Достаточность доказана. Теорема доказана.
выпуклый на множестве U. Достаточность доказана. Теорема доказана.
Теорема 4. Пусть  – выпуклое множество банахова пространства X. Для того, чтобы функционал
– выпуклое множество банахова пространства X. Для того, чтобы функционал  был выпуклым на U, необходимо и достаточно, чтобы выполнялось неравенство
был выпуклым на U, необходимо и достаточно, чтобы выполнялось неравенство
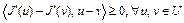 . (6)
. (6)
Доказательство. Необходимость. Пусть 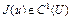 выпуклый функционал на U. Покажем, что выполнено неравенство (6). В самом деле, из (3) следует, что
выпуклый функционал на U. Покажем, что выполнено неравенство (6). В самом деле, из (3) следует, что
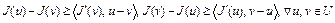 .
.
После сложения этих неравенств получим
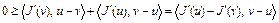 .
.
Отсюда имеем 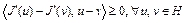 . Необходимость доказана.
. Необходимость доказана.
Достаточность. Пусть выполнено неравенство (6). Покажем, что  выпуклый функционал на U. Рассмотрим разность
выпуклый функционал на U. Рассмотрим разность

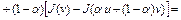
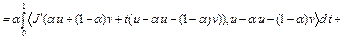
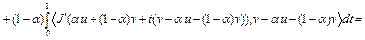
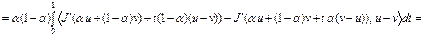
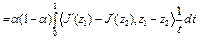 ,
,
где 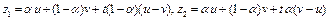 . Отсюда с учетом того, что
. Отсюда с учетом того, что 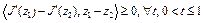 , имеем
, имеем  , т.е.
, т.е. 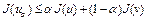 ,
, 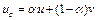 . Это означает, что функционал
. Это означает, что функционал  выпуклый на U. Достаточность доказана. Теорема доказана.
выпуклый на U. Достаточность доказана. Теорема доказана.
Теперь рассмотрим дважды непрерывно дифференцируемый функционал  , определенный на выпуклом множестве U.
, определенный на выпуклом множестве U.
Определение 9. Пусть функционал  определен в
определен в 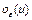 окрестности точки
окрестности точки 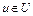 . Функционал
. Функционал  дважды дифференцируем в точке
дважды дифференцируем в точке 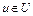 по Фреше, если
по Фреше, если
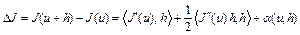 ,
,
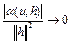 при
при 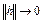 ,
,
где 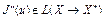 – вторая производная
– вторая производная  в точке u. Квадратичная форма
в точке u. Квадратичная форма  называется вторым дифференциалом
называется вторым дифференциалом  в точке u. Функционал
в точке u. Функционал  дважды непрерывно дифференцируем на множестве U банахова пространства X, если он дважды дифференцируем во всех точках
дважды непрерывно дифференцируем на множестве U банахова пространства X, если он дважды дифференцируем во всех точках 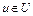 и
и 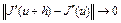 при
при 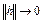 .
.
Множество всех функционалов, дважды непрерывно дифференцируемых на U, обозначим через 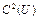 .
.
Теорема 5. Пусть 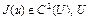 – выпуклое множество банахова пространства X. Для того, чтобы функционал
– выпуклое множество банахова пространства X. Для того, чтобы функционал 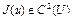 был выпуклым на U,
был выпуклым на U, 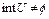 , необходимо и достаточно, чтобы
, необходимо и достаточно, чтобы
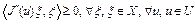 . (7)
. (7)
Доказательство. Необходимость. Пусть 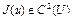 выпуклый на U. Покажем, что выполнено (7). Если
выпуклый на U. Покажем, что выполнено (7). Если 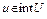 , то
, то 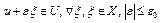 .
.
Так как выполнены предпосылки теоремы 4,  , то верно неравенство
, то верно неравенство
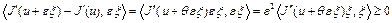 , где
, где 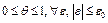 . Отсюда при
. Отсюда при 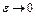 получим неравенство (7) для всех
получим неравенство (7) для всех 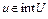 . Если
. Если 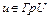 – граничная точка, то существует последовательность
– граничная точка, то существует последовательность 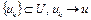 при
при  такая, что
такая, что 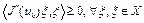 . Отсюда, переходя к пределу, с учетом непрерывности
. Отсюда, переходя к пределу, с учетом непрерывности 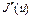 получим (7). Необходимость доказана.
получим (7). Необходимость доказана.
Достаточность. Пусть 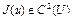 и выполнено неравенство (7). Покажем, что функционал
и выполнено неравенство (7). Покажем, что функционал  выпуклый на множестве U. Как следует из формулы конечных приращений Лагранжа, верно равенство
выпуклый на множестве U. Как следует из формулы конечных приращений Лагранжа, верно равенство
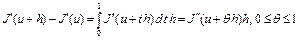 .
.
Тогда
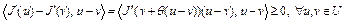
в силу (7), где 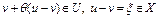 . Таким образом, функционал
. Таким образом, функционал 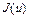 на U удовлетворяет условию
на U удовлетворяет условию
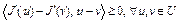 .
.
Как следует из теоремы 4, функционал 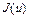 выпуклый на U. Достаточность доказана. Теорема доказана.
выпуклый на U. Достаточность доказана. Теорема доказана.
ЛЕКЦИЯ 7.СИЛЬНО ВЫПУКЛЫЕ ФУНКЦИОНАЛЫ
Рассмотрим свойства гладких функционалов  на выпуклом множестве U гильбертова пространства H.
на выпуклом множестве U гильбертова пространства H.
Теорема 1. Пусть  – выпуклое множество гильбертова пространства H. Для того, чтобы функционал
– выпуклое множество гильбертова пространства H. Для того, чтобы функционал 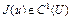 был сильно выпуклым на U, необходимо и достаточно, чтобы выполнялось неравенство
был сильно выпуклым на U, необходимо и достаточно, чтобы выполнялось неравенство
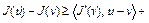
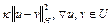 , (1) где
, (1) где 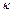 =const>0 –коэффициент сильной выпуклости.
=const>0 –коэффициент сильной выпуклости.
Доказательство. Необходимость. Пусть 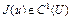 – сильно выпуклый функционал на множестве
– сильно выпуклый функционал на множестве 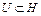 . Покажем, что верно неравенство (1).
. Покажем, что верно неравенство (1).
Поскольку  сильно выпуклый функционал, то, по определению, верно неравенство
сильно выпуклый функционал, то, по определению, верно неравенство
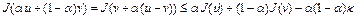
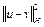 ,
, 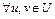 , где
, где 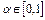 . Отсюда имеем
. Отсюда имеем
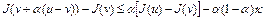
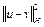 ,
, 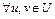 ,
, 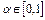 . Так как по формуле конечных приращений Лагранжа разность
. Так как по формуле конечных приращений Лагранжа разность
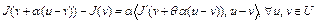 ,
,
то
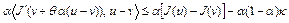
 .
.
Отсюда после деления на 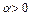 и при
и при  получим неравенство (1). Необходимость доказана.
получим неравенство (1). Необходимость доказана.
Достаточность. Пусть выполнено неравенство (1). Покажем, что функционал 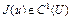 сильно выпуклый. В самом деле, из (1) имеем
сильно выпуклый. В самом деле, из (1) имеем

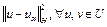 ,
,
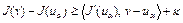
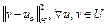 ,
,
где 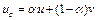 . Умножим первое неравенство на величину
. Умножим первое неравенство на величину 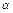 , а второе на неравенство
, а второе на неравенство  и, сложив их, получим
и, сложив их, получим
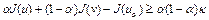
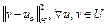 ,
,
где
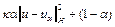
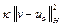 =
= 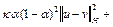
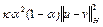 = =
= = 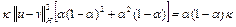
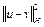 .
.
Тогда
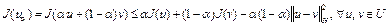 .
.
Это означает, что функционал  сильно выпуклый на U. Достаточность доказана. Теорема доказана.
сильно выпуклый на U. Достаточность доказана. Теорема доказана.
Теорема 2. Пусть  – выпуклое множество гильбертова пространства H. Для того, чтобы функционал
– выпуклое множество гильбертова пространства H. Для того, чтобы функционал 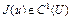 был сильно выпуклым на U, необходимо и достаточно, чтобы выполнялось неравенство
был сильно выпуклым на U, необходимо и достаточно, чтобы выполнялось неравенство
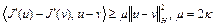
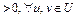 . (2)
. (2)
Доказательство. Необходимость. Пусть 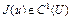 сильно выпуклый функционал на
сильно выпуклый функционал на 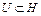 . Покажем, что выполнено неравенство (2). Действительно, из теоремы 1 следует, что
. Покажем, что выполнено неравенство (2). Действительно, из теоремы 1 следует, что
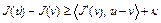
 ,
,
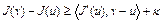
 ,
,
После сложения этих неравенств получим
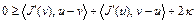
 .
.
Отсюда следует неравенство (2). Необходимость доказана.
Достаточность. Пусть выполнено неравенство (2). Покажем, что функционал 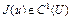 сильно выпуклый на множестве
сильно выпуклый на множестве 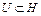 . Как следует из доказательства теоремы 4 лекции 6, верно равенство
. Как следует из доказательства теоремы 4 лекции 6, верно равенство
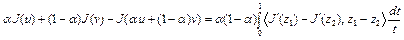 ,(3) где
,(3) где 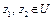 . Согласно неравенству (2), верна оценка
. Согласно неравенству (2), верна оценка
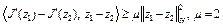
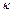 .
.
Тогда из (3) следует, что
 .
.
Отсюда с учетом того, что разность 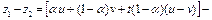
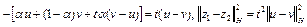 , получим
, получим
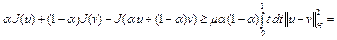

 .
.
Следовательно,
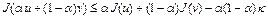
 .
.
Это означает, что функционал 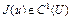 сильно выпуклый на множестве U. Достаточность доказана. Теорема доказана.
сильно выпуклый на множестве U. Достаточность доказана. Теорема доказана.
Теорема 3. Пусть 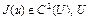 – выпуклое множество гильбертова пространства H. Для того, чтобы функционал
– выпуклое множество гильбертова пространства H. Для того, чтобы функционал  был сильно выпуклым на U, необходимо и достаточно, чтобы
был сильно выпуклым на U, необходимо и достаточно, чтобы
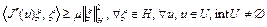 , (4) где
, (4) где 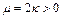 .
.
Дата добавления: 2015-08-21; просмотров: 1549;
