Глава 7. Краевые задачи оптимального управления………………..226 6 страница
Доказательство. Необходимость. Пусть 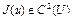 сильно выпуклый функционал на U. Покажем, что верно неравенство (4). В самом деле, если
сильно выпуклый функционал на U. Покажем, что верно неравенство (4). В самом деле, если 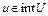 , то для любого
, то для любого 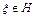 точка
точка 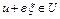 при всех
при всех 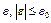 . Тогда из (2) с учетом того, что
. Тогда из (2) с учетом того, что 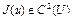 , имеем
, имеем
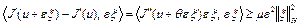 ,
,
при всех 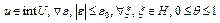 . Отсюда следует, что
. Отсюда следует, что 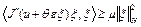 . Тогда при
. Тогда при 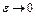 верно неравенство (4). Необходимость доказана.
верно неравенство (4). Необходимость доказана.
Достаточность. Пусть 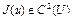 и выполнено неравенство (4). Покажем, что функционал
и выполнено неравенство (4). Покажем, что функционал  сильно выпуклый на U. Для любых
сильно выпуклый на U. Для любых 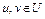 , точка
, точка  . Используя формулу конечных приращений Лагранжа, получим
. Используя формулу конечных приращений Лагранжа, получим
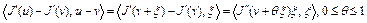 .
.
Отсюда с учетом того, что 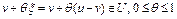 , и неравенства (4), получим
, и неравенства (4), получим
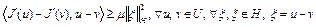 .
.
Таким образом, функционал 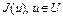 удовлетворяет условию (2). Это означает, что функционал
удовлетворяет условию (2). Это означает, что функционал  сильно выпуклый на U. Достаточность доказана. Теорема доказана.
сильно выпуклый на U. Достаточность доказана. Теорема доказана.
Теорема 4. Пусть U – выпуклое замкнутое множество из гильбертова пространства H, функционал  сильно выпуклый и полунепрерывен снизу на U. Тогда:
сильно выпуклый и полунепрерывен снизу на U. Тогда:
1) множество Лебега 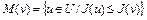 выпукло, замкнуто и ограничено при всех
выпукло, замкнуто и ограничено при всех 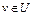 ;
;
2) верно неравенство
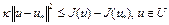 , (5) где
, (5) где 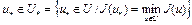 .
.
Доказательство. Покажем, что множество 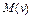 выпукло, замкнуто и ограничено. Возьмем произвольную точку
выпукло, замкнуто и ограничено. Возьмем произвольную точку 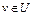 . Тогда
. Тогда 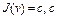 – некоторое число. Легко убедиться в том, что множество
– некоторое число. Легко убедиться в том, что множество 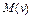 – выпукло. В самом деле, для любых
– выпукло. В самом деле, для любых 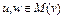 , т.е.
, т.е. 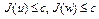 , в точке
, в точке 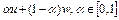 , значение
, значение
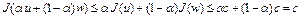 ,
,
в силу выпуклости функционала  . Отсюда следует, что
. Отсюда следует, что 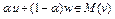 . Следовательно, множество
. Следовательно, множество 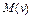 выпукло.
выпукло.
Можно показать, что множество 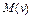 замкнуто. Пусть u – предельная точка множества
замкнуто. Пусть u – предельная точка множества 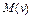 . Тогда существует последовательность
. Тогда существует последовательность 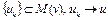 при
при  . Поскольку функционал полунепрерывен снизу на множестве U, то он полунепрерывен снизу на
. Поскольку функционал полунепрерывен снизу на множестве U, то он полунепрерывен снизу на 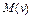 , где
, где 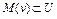 . Тогда
. Тогда
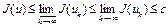 ,
,
в силу того, что 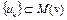 , т.е.
, т.е.  . Отсюда следует, что
. Отсюда следует, что 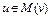 . Следовательно, множество
. Следовательно, множество 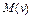 – замкнуто.
– замкнуто.
Покажем, что множество 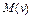 ограничено. Пусть
ограничено. Пусть 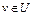 – любая фиксированная точка,
– любая фиксированная точка, 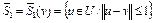 – единичный замкнутый шар. Обозначим через
– единичный замкнутый шар. Обозначим через 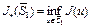 . Тогда для любой точки
. Тогда для любой точки 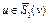 значение
значение 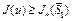 . Пусть величина
. Пусть величина 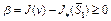 , т.е.
, т.е. 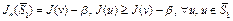 . Введем множество
. Введем множество 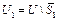 . Если
. Если 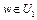 , то
, то 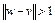 . Тогда величина
. Тогда величина
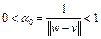 . (6)
. (6)
Поскольку  сильно выпуклый функционал, то верно неравенство
сильно выпуклый функционал, то верно неравенство

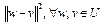 .
.
Отсюда при 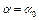 имеем
имеем
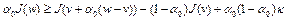
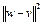 . (7)
. (7)
Как следует из (6), 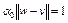 . Тогда
. Тогда 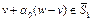 , в силу того, что
, в силу того, что 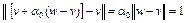 . Поскольку
. Поскольку 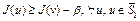 , то, в частности, для точки
, то, в частности, для точки 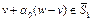 имеем
имеем 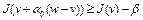 . Теперь неравенство (7) запишется в виде
. Теперь неравенство (7) запишется в виде
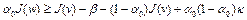
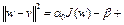
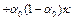
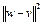 .
.
Отсюда, после деления на 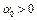 , имеем
, имеем
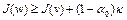
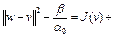
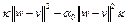
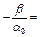
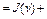
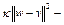
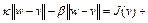
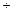
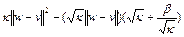 , (8) где
, (8) где 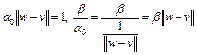 . Так как
. Так как
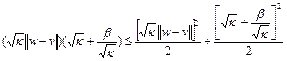 ,
,
то из (8) следует, что
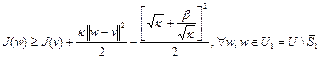 . (9)
. (9)
Легко убедиться в том, что неравенство (9) верно и для 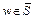 . В самом деле, если
. В самом деле, если 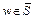 , то
, то 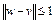 . Следовательно, верно неравенство
. Следовательно, верно неравенство
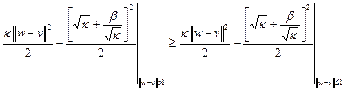 .
.
Тогда из (9) следует, что
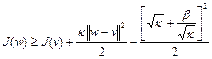 , при
, при 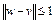 . (10)
. (10)
Из (9) и (10) следует, что
 . (11)
. (11)
Поскольку множество 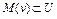 , то неравенство (11) верно для всех
, то неравенство (11) верно для всех 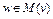 . Так как множество
. Так как множество 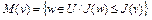 , то из (11) имеем
, то из (11) имеем
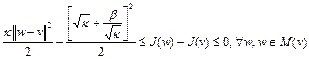 .
.
Тогда
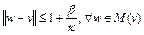 .
.
Это означает, что множество 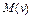 ограничено. Итак, доказано первое утверждение теоремы.
ограничено. Итак, доказано первое утверждение теоремы.
Покажем, что верно неравенство (5). Поскольку функционал  сильно выпуклый, то из определения сильной выпуклости имеем
сильно выпуклый, то из определения сильной выпуклости имеем 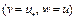
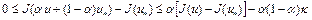
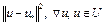 .
.
Следовательно,
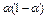
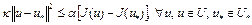 .
.
Отсюда, после деления на 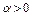 и
и 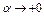 , получим неравенство (5). Теорема доказана.
, получим неравенство (5). Теорема доказана.
Определение. Функционал  , определенный на выпуклом множестве U банахова пространства X, называется равномерно выпуклым на U, если
, определенный на выпуклом множестве U банахова пространства X, называется равномерно выпуклым на U, если
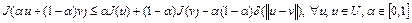 , где
, где 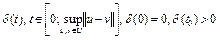 для некоторого
для некоторого 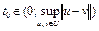 называется модулем выпуклости
называется модулем выпуклости  на U. Если
на U. Если 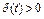 при всех
при всех 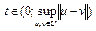 , то такой функционал
, то такой функционал  называется строго равномерно выпуклым.
называется строго равномерно выпуклым.
Функцию
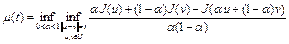
называют точным модулем выпуклости  на U.
на U.
Заметим, что: 1) любой сильно выпуклый функционал  на U является строго равномерно выпуклым, причем модуль выпуклости
на U является строго равномерно выпуклым, причем модуль выпуклости 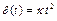 ;
;
2) в гильбертовом пространстве H функционалы 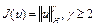 – строго равномерно выпуклые, где
– строго равномерно выпуклые, где 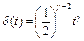 .
.
Теорема 5. Пусть U – выпуклое замкнутое множество из гильбертова пространства H, функционал  равномерно выпуклый и полунепрерывен снизу на U. Тогда:
равномерно выпуклый и полунепрерывен снизу на U. Тогда:
1) множество Лебега 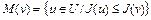 выпукло, замкнуто и ограничено при всех
выпукло, замкнуто и ограничено при всех 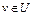 ;
;
2) верно неравенство
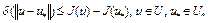 .
.
Доказательство теоремы аналогично доказательству теоремы 4.
ЛЕКЦИЯ 8.ТЕОРЕМА О ГЛОБАЛЬНОМ МИНИМУМЕ. УСЛОВИЯ ОПТИМАЛЬНОСТИ. ПРОЕКЦИЯ ТОЧКИ НА МНОЖЕСТВО
Теорема о глобальном минимуме. Рассмотрим задачу оптимального управления
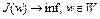 , (1) где
, (1) где  – функционал, определенный на множестве W банахова пространства X.
– функционал, определенный на множестве W банахова пространства X.
Теорема 1. Если  – выпуклый функционал, определенный на выпуклом множестве W банахова пространства X, то любая точка локального минимума функционала
– выпуклый функционал, определенный на выпуклом множестве W банахова пространства X, то любая точка локального минимума функционала  на W одновременно является точкой его глобального минимума на W, причем множество
на W одновременно является точкой его глобального минимума на W, причем множество 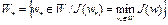 выпукло. Если
выпукло. Если  строго выпуклый функционал на выпуклом множестве W, то множество
строго выпуклый функционал на выпуклом множестве W, то множество 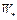 содержит не более одной точки.
содержит не более одной точки.
Доказательство. Пусть 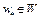 – точка локального минимума функционала
– точка локального минимума функционала  на выпуклом множестве W, т.е.
на выпуклом множестве W, т.е. 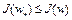 при всех
при всех 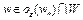 , где
, где 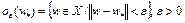 . Покажем, что в точке
. Покажем, что в точке 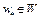 достигается абсолютный минимум функционала
достигается абсолютный минимум функционала  на W, т.е.
на W, т.е. 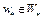 .
.
Пусть 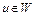 – произвольная точка. Тогда точка
– произвольная точка. Тогда точка 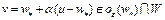 в силу выпуклости множества W, если
в силу выпуклости множества W, если 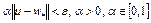 . Следовательно, выполняется неравенство
. Следовательно, выполняется неравенство 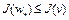 . С другой стороны, поскольку
. С другой стороны, поскольку  – выпуклый функционал на W, то имеет место неравенство
– выпуклый функционал на W, то имеет место неравенство
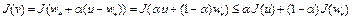 .
.
Теперь неравенство 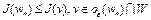 запишется в виде
запишется в виде
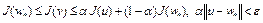 .
.
Отсюда следует, что 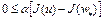 . Тогда
. Тогда 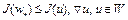 . Это означает, что в точке
. Это означает, что в точке 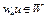 достигается глобальный (или абсолютный) минимум функционала
достигается глобальный (или абсолютный) минимум функционала  на W.
на W.
Покажем, что множество 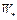 выпукло. В самом деле, для любых
выпукло. В самом деле, для любых 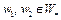 , т.е.
, т.е. 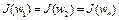 , и при всех
, и при всех 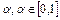 значение
значение 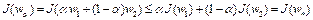 . Следовательно,
. Следовательно, 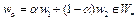 . Выпуклость множества
. Выпуклость множества 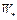 доказана. Заметим, что если
доказана. Заметим, что если 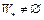 , то
, то 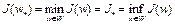 .
.
Пусть  – строго выпуклый функционал на выпуклом множестве W. Покажем, что множество
– строго выпуклый функционал на выпуклом множестве W. Покажем, что множество 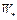 содержит единственную точку. В самом деле,
содержит единственную точку. В самом деле,
 ,
,
если множество 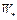 содержит точки
содержит точки  . Противоречие
. Противоречие 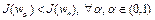 снимается, если
снимается, если 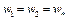 , т.е. множество
, т.е. множество 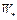 содержит не более одной точки. Теорема доказана.
содержит не более одной точки. Теорема доказана.
Из данной теоремы следует, что выпуклый функционал  на выпуклом множестве W не может иметь локальных минимумов, отличных от точек глобального минимума.
на выпуклом множестве W не может иметь локальных минимумов, отличных от точек глобального минимума.
Условия оптимальности. Рассмотрим задачу оптимального управления
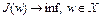 , (2) где X – банахово пространство. Для задачи (2) условия оптимальности дает следующая теорема.
, (2) где X – банахово пространство. Для задачи (2) условия оптимальности дает следующая теорема.
Теорема 2. Пусть множество 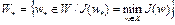 . Если функционал
. Если функционал  дифференцируем по Фреше в точке
дифференцируем по Фреше в точке 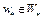 , то необходимо выполняется равенство
, то необходимо выполняется равенство
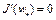 , (3) а если
, (3) а если  дважды дифференцируем по Фреше в точке
дважды дифференцируем по Фреше в точке 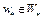 , то необходимо выполняются соотношения
, то необходимо выполняются соотношения
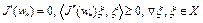 . (4)
. (4)
Доказательство. Пусть 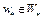 – точка глобального минимума. Тогда для любого
– точка глобального минимума. Тогда для любого  и при всех
и при всех 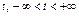 приращение функционала
приращение функционала 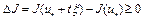 . Поскольку функционал
. Поскольку функционал  дифференцируем в точке
дифференцируем в точке 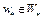 , то
, то
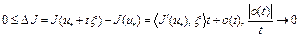 при
при 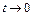 .
.
Отсюда следует, что 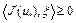 при
при 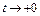 и
и 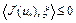 при
при  . Следовательно,
. Следовательно, 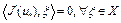 . Это возможно тогда и только тогда, когда
. Это возможно тогда и только тогда, когда 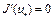 . Утверждение (3) доказано.
. Утверждение (3) доказано.
Если функционал  дважды дифференцируем в точке
дважды дифференцируем в точке 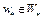 , то
, то
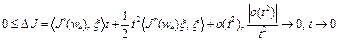 .
.
Так как 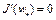 , то выполняется неравенство
, то выполняется неравенство
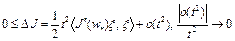 при
при  .
.
Отсюда, после деления на 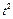 , получим
, получим 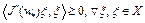 . Утверждение (4) доказано. Теорема доказана.
. Утверждение (4) доказано. Теорема доказана.
Теперь рассмотрим задачу оптимального управления (1). Следующая теорема дает условия оптимальности для задачи (1).
Теорема 3. Пусть W – выпуклое множество банахова пространства X, функционал 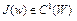 , множество
, множество 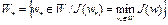 . Тогда в любой точке
. Тогда в любой точке 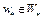 необходимо выполняется неравенство
необходимо выполняется неравенство
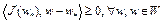 . (5)
. (5)
Если 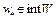 , то неравенство (5) равносильно тому, что
, то неравенство (5) равносильно тому, что 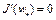 . Кроме того, если
. Кроме того, если 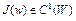 выпуклый функционал, то в любой точке
выпуклый функционал, то в любой точке 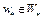 необходимо и достаточно выполнение неравенства (5).
необходимо и достаточно выполнение неравенства (5).
Доказательство. Необходимость. Пусть точка 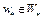 . Покажем, что выполнено неравенство (5), где W – выпуклое множество банахова пространства X.
. Покажем, что выполнено неравенство (5), где W – выпуклое множество банахова пространства X.
Пусть 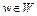 – произвольная точка и число
– произвольная точка и число 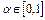 . Точка
. Точка  в силу выпуклости множества W. Так как
в силу выпуклости множества W. Так как 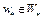 , то
, то 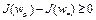 . Отсюда следует, что
. Отсюда следует, что

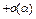 , причем
, причем 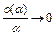 при
при 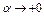 . Делим обе части на
. Делим обе части на 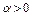 и, переходя к пределу при
и, переходя к пределу при 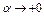 , получим неравенство (5). Неравенство (5) верно, в частности, когда
, получим неравенство (5). Неравенство (5) верно, в частности, когда 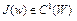 – выпуклый функционал. Итак, доказано первое утверждение теоремы.
– выпуклый функционал. Итак, доказано первое утверждение теоремы.
Если 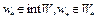 , то найдется число
, то найдется число 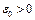 такое, что для любого
такое, что для любого  точка
точка 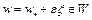 при всех
при всех 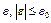 . Тогда из (5) следует, что
. Тогда из (5) следует, что 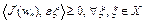 и при всех
и при всех 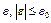 .
.
Отсюда имеем 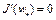 . Необходимость доказана.
. Необходимость доказана.
Достаточность. Пусть 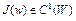 – выпуклый функционал, W – выпуклое множество,
– выпуклый функционал, W – выпуклое множество, 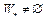 и выполнено неравенство (5). Покажем, что
и выполнено неравенство (5). Покажем, что 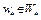 .
.
Пусть 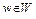 – произвольная точка. Так как
– произвольная точка. Так как 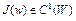 – выпуклый функционал, то для любых точек
– выпуклый функционал, то для любых точек 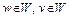 необходимо и достаточно выполнение неравенства (см. теорему 3, лекция 6)
необходимо и достаточно выполнение неравенства (см. теорему 3, лекция 6)
 .
.
Отсюда при 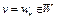 имеем
имеем
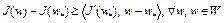 . (6)
. (6)
Так как выполнено неравенство (5), то 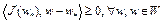 . Тогда из (6) имеем
. Тогда из (6) имеем 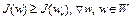 . Это означает, что
. Это означает, что 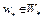 . Достаточность доказана. Теорема доказана.
. Достаточность доказана. Теорема доказана.
Пусть функционал  определен в
определен в 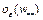 окрестности точки
окрестности точки 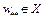 . Говорят, что
. Говорят, что  достигает в точке
достигает в точке 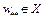 локального минимума, если в окрестности
локального минимума, если в окрестности 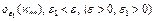 точки
точки 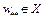 выполняется неравенство
выполняется неравенство 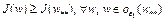 .
.
Теорема 4. Пусть функционал  определен в
определен в 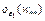 окрестности точки
окрестности точки 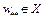 . Для того, чтобы точка
. Для того, чтобы точка 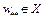 была точкой локального минимума функционала
была точкой локального минимума функционала  , имеющего слабый дифференциал, необходимо, чтобы
, имеющего слабый дифференциал, необходимо, чтобы 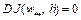 .
.
Доказательство. Как следует из определения дифференциала Гато (или слабого дифференциала (см. лекцию 2)), для любого 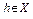 имеем
имеем
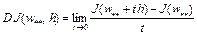 .
.
Рассмотрим скалярную функцию 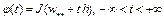 . Поскольку функция
. Поскольку функция 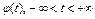 имеет локальный минимум в точке
имеет локальный минимум в точке 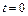 , то
, то
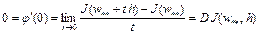 .
.
Теорема доказана.
Заметим, что если функционал  дифференцируем по Гато (по Фреше) в точке
дифференцируем по Гато (по Фреше) в точке 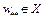 , то
, то 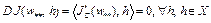 . Тогда
. Тогда 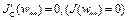 .
.
Дата добавления: 2015-08-21; просмотров: 1332;
