Слабая компактность.

Определение 1. Множество U банахова пространства X называется слабо компактным, если из любой последовательности 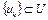можно выбрать хотя бы одну подпоследовательность, которая слабо в X сходится к некоторой точке 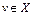. Если точка 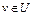, то множество U слабо бикомпактно.

Определение 2. Последовательность 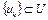называется слабо фундаментальной, если для любого 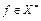числовая последовательность 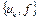фундаментальна. Пространство X называется слабо полным, если всякая слабо фундаментальная в X последовательность является слабо сходящейся.

Теорема 1. В банаховом пространстве всякое слабо ограниченное множество U является ограниченным.

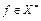Доказательство. Множество называется слабо ограниченным, если для любого числовое множество ограничено. Отметим, что если последовательность 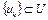слабо сходится к элементу 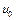, то – ограничена. Предположим противное, т.е. множество U слабо ограничено, но оно не ограничено. Тогда существует последовательность 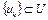такая, что 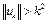. Формируем последовательность 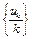. Тогда для любого 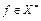числовая последовательность 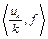обладает свойством

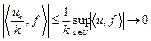при ,

в силу того, что множество U слабо ограничено. Из данного неравенства следует, что последовательность 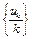при слабо сходится к элементу 0. Так как слабо сходящаяся последовательность ограничена, то 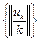ограничена. Это противоречит тому, что 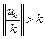. Теорема доказана.

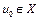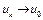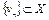Теорема 2 (теорема Мазура). Пусть последовательность – банахово пространство, слабо сходится к элементу , т.е. слабо при . Тогда существует последовательность , где

,

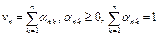составленная из выпуклых линейных комбинаций точек 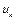, такая, что сильно при .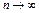

Доказательство. Пусть U – множество всевозможных конечных выпуклых комбинаций точек 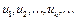. Множество U и его замыкания 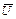– выпуклые множества. По утверждению теоремы, точка 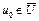. Предположим противное, т.е. 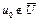. Тогда множество 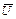и точка 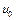сильно отделимы (см. лекция 9, теорема 1). Это значит, что найдется элемент 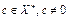, такой, что . В частности, поскольку 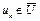, то . Это противоречит тому, что 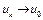слабо при . Теорема доказана.

Теорема 3. Любое слабо компактное множество U банахова пространства X ограничено.

Доказательство. Пусть множество U слабо компактно. Покажем, что оно ограничено. Предположим противное, т.е. множество U не ограничено. Тогда существует последовательность 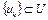такая, что 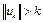. Так как множество U слабо компактно, то найдется подпоследовательность 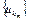, которая слабо сходится к некоторой точке 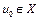, т.е. слабо при 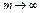. Как следует из доказательства теоремы 1, последовательность 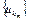ограничена. Это противоречит тому, что 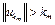. Следовательно, множество U ограничено. Теорема доказана.

Теорема 4. Любое ограниченное множество U рефлексивного банахова пространства X слабо компактно.

Доказательство. Пусть U ограниченное множество рефлексивного банахова пространства X. Банахово пространство X рефлексивно, если 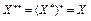. Покажем, что множество U слабо компактно, т.е. любая последовательность 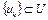слабо сходится.

Рассмотрим всевозможные конечные комбинации элементов последовательности 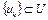. Пусть множество V является замыканием всевозможных конечных линейных комбинаций элементов последовательности 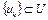. Множество V – подпространство рефлексивного банахова пространства X. Так как V содержит счетный базис, то V сепарабельно и, как подпространство рефлексивного банахова пространства X, подпространство V рефлексивно, т.е. 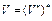. Тогда подпространство 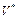также сепарабельно. Пусть 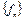– счетный базис в .

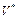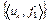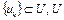Рассмотрим числовую последовательность . Она ограничена, так как , в силу того, что – ограниченное множество. Тогда, согласно теореме Больцано-Вейерштрасса, можно выделить сходящуюся подпоследовательность 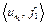, где – подпоследовательность последовательности .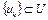

Теперь строим числовую последовательность . Она ограничена и, значит, содержит сходящуюся подпоследовательность 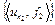и т.д. Повторяя данную процедуру, строим последовательности 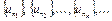, причем

Строим диагональную последовательность , где k-член равен k-члену последовательности . Заметим, что числовые последовательности 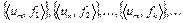сходятся как подпоследовательности сходящихся последовательностей.

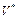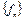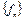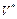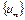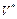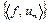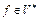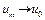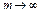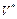Тогда последовательность слабо сходится на плотном в множестве , где – счетное, всюду плотное в множество. Так как V рефлексивно, то можно считать последовательностью линейных функционалов в . Тогда, по теореме Банаха-Штейнгауза, числовая последовательность сходится для любого . Итак, слабо при на . Так как 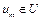, то по теореме Мазура элемент .

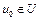Пусть теперь 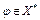. Его сужение на 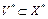обозначим через 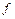. Тогда

.

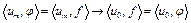Это означает, что последовательность 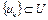слабо сходится к элементу 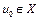. Следовательно, множество U слабо компактно. Теорема доказана.

Определение 2. Множество U банахова пространства X называется слабо замкнутым, если оно содержит все свои слабо предельные точки.

Теорема 5. Любое ограниченное слабо замкнутое множество U из рефлексивного банахова пространства X слабо бикомпактно.

Доказательство. Как следует из теоремы 4, множество U слабо компактно. Так как оно содержит все свои слабо предельные точки, то U слабо бикомпактно. Теорема доказана.

Теорема 6. Любое ограниченное замкнутое выпуклое множество U из рефлексивного банахова пространства X слабо бикомпактно.

Доказательство. Как следует из теоремы 4, множество U слабо компактно. Покажем, что множество U слабо замкнуто. Берем произвольную последовательность 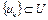. Так как множество U слабо компактно, то из 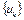можно выделить подпоследовательность 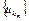, которая слабо сходится к некоторой точке 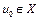. Для доказательства теоремы достаточно показать, что точка .

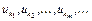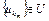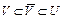Пусть множество V содержит всевозможные конечные выпуклые комбинации точек последовательности . Множество V и его замыкание выпуклы, причем в силу того, что U – выпуклое замкнутое множество. Покажем, что слабо предельная точка .

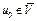Предположим противное, т.е. точка 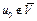. Тогда множество V и точка 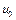сильно отделимы. Следовательно, существует гиперплоскость 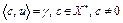такая, что 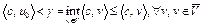. Так как 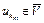, то, в частности, имеем 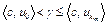при всех 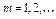. Это противоречит тому, что последовательность 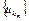слабо сходится к точке 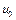. Следовательно, 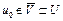. Таким образом, доказана слабая замкнутость множества U. Тогда из теоремы 5 следует, что множество U слабо бикомпактно. Теорема доказана.

Пример 1. Множество – замкнутый шар в гильбертовом пространстве H, слабо бикомпактно, так как оно ограниченное выпуклое замкнутое множество в рефлексивном банаховом пространстве H.

Пример 2. Множество 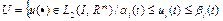, , 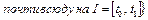где 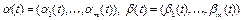– известные непрерывные функции, слабо бикомпактно, так как U ограниченное замкнутое выпуклое множество в рефлексивном банаховом пространстве .

Слабая полунепрерывность снизу функционала. Рассмотрим задачу оптимального управления

, (1) где U – слабо бикомпактное множество. Возникает вопрос: при выполнении каких условий функционал 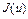будет слабо полунепрерывен снизу на множестве U? Положительный ответ на данный вопрос дает следующая теорема.

Теорема 7. Пусть 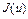– выпуклый функционал, определенный на выпуклом множестве U банахова пространства X. Тогда функционал 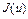слабо полунепрерывен снизу на множестве U тогда и только тогда, когда 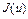полунепрерывен снизу на множестве U.

Доказательство. Необходимость. Пусть функционал 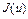слабо полунепрерывен снизу на U. Покажем, что 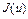полунепрерывен снизу на U. Поскольку U выпуклое множество, то оно не имеет изолированных точек. Следовательно, если точка , то существует последовательность 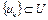, которая сильно сходится к точке u, т.е. 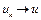при 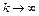. Тогда последовательность 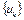слабо сходится к точке u, т.е. 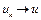при 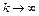слабо. Так как функционал 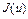слабо полунепрерывен снизу на множестве U, то

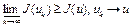при 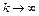слабо.

Отсюда и из сильной сходимости последовательности 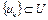к точке u, имеем

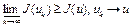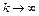при сильно.

Это означает, что функционал 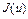полунепрерывен снизу на множестве U. Необходимость доказана.

Достаточность. Пусть выпуклый функционал 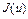полунепрерывен снизу на выпуклом множестве U. Покажем, что 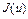слабо полунепрерывен снизу на U.

Пусть последовательность 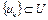слабо сходится к точке . Рассмотрим числовую последовательность 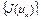. Обозначим нижний предел числовой последовательности 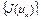, равный 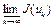. Для простоты обозначения полагаем, что 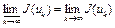. (В самом деле, 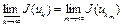). Как следует из теоремы Мазура (см. теорему 2), точка принадлежит замыканию выпуклой оболочки точек . Иными словами, для каждого k найдется целое число m, 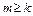, и числа 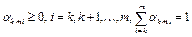такие, что последовательность , где 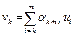, сильно сходится к точке u, т.е. 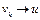при 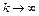сильно.

Так как функционал 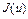полунепрерывен снизу в точке u, то выполняется неравенство

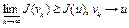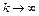при сильно.

Поскольку 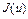– выпуклый функционал на выпуклом множестве U, точки , то (см. лекцию 6)

.

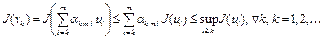Отсюда с учетом того, что

,

получим

.

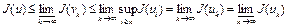Следовательно,

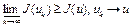при 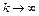слабо.

Это означает, что функционал 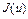слабо полунепрерывен снизу на выпуклом множестве U. Достаточность доказана. Теорема доказана.

Напомним, что в лекции 5 была доказана теорема 4 (теорема Вейерштрасса) о том, что: если U слабо бикомпактно, функционал 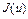слабо полунепрерывен снизу на U, то: 1) 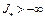; 2) 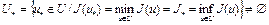, слабо бикомпактно; 3) любая минимизирующая последовательность 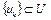слабо сходится к множеству .

Также были доказаны следующие факты: а) любое ограниченное замкнутое выпуклое множество U из рефлексивного банахова пространства X слабо бикомпактно (см. теорема 6); б) выпуклый, полунепрерывный снизу функционал 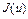на выпуклом множестве U слабо полунепрерывен снизу.

Теперь теорема 4 из лекции 5 может быть сформулирована следующим образом.

Теорема 8. Пусть U – выпуклое замкнутое ограниченное множество из рефлексивного банахова пространства X, выпуклый функционал 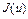определен, конечен и полунепрерывен снизу на U. Тогда:

1) 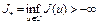(ограничен снизу);

2) множество 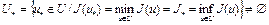, выпукло, замкнуто и ограничено;

3) любая минимизирующая последовательность слабо сходится к .

В отличие от теоремы 4 из лекции 5, условия теоремы 8 могут быть легко проверены.

довательно, сти слабого предела, имеем – е м следовательности слабо сходится к элементу ества м. ательность сходится к множеству сти принадлежит множеству