Глава 7. Краевые задачи оптимального управления………………..226 7 страница
Теорема 5. Пусть функционал 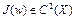 , т.е.
, т.е.
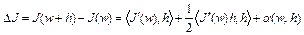 ,
,
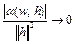 при
при 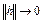 .
.
Для того, чтобы точка 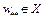 была точкой локального минимума, достаточно выполнение следующих условий:
была точкой локального минимума, достаточно выполнение следующих условий:
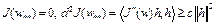 ,
,
где 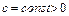 .
.
Доказательство. Как следует из теоремы 2, производная по Фреше 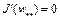 , тогда
, тогда
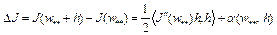 , (7) где
, (7) где 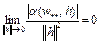 . По условию теоремы
. По условию теоремы 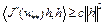 . Выберем величину
. Выберем величину 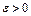 так, чтобы при
так, чтобы при 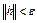 величина
величина 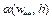 из (7) удовлетворяла условию
из (7) удовлетворяла условию 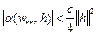 . Тогда
. Тогда 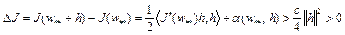 при
при 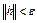 . Отсюда следует, что
. Отсюда следует, что 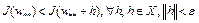 . Это означает, что в точке
. Это означает, что в точке 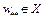 достигается локальный минимум. Теорема доказана.
достигается локальный минимум. Теорема доказана.
Проекция точки на множество. В качестве приложения к теоремам 1,3 рассмотрим проекцию точки на выпуклом замкнутом множестве W банахова пространства X.
Определение. Пусть W – некоторое множество из X, а точка 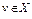 . Точка
. Точка 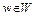 называется проекцией точки
называется проекцией точки 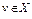 на множестве W, если норма
на множестве W, если норма 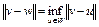 , и обозначается
, и обозначается 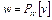 .
.
Теорема 6. Пусть W – выпуклое замкнутое множество из гильбертова пространства H. Тогда
1) любая точка 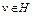 имеет единственную проекцию на множестве W;
имеет единственную проекцию на множестве W;
2) для того, чтобы точка 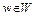 была проекцией точки
была проекцией точки 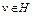 на множестве W, необходимо и достаточно выполнение неравенства
на множестве W, необходимо и достаточно выполнение неравенства
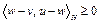 при всех
при всех 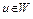 ; (8)
; (8)
3) справедливо неравенство
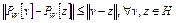 . (9)
. (9)
Доказательство. Квадрат расстояния от точки 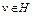 до точки
до точки 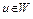 равен
равен 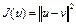 . При фиксированном
. При фиксированном 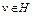 функционал
функционал  – сильно выпуклый на выпуклом замкнутом множестве W. Любой сильно выпуклый функционал является строго выпуклым. Тогда согласно теореме 1 функционал
– сильно выпуклый на выпуклом замкнутом множестве W. Любой сильно выпуклый функционал является строго выпуклым. Тогда согласно теореме 1 функционал  достигает нижней грани в единственной точке w, причем
достигает нижней грани в единственной точке w, причем 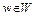 в силу ее замкнутости. Следовательно, точка
в силу ее замкнутости. Следовательно, точка 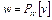 .
.
Поскольку точка 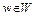 – точка глобального минимума функционала
– точка глобального минимума функционала  на множестве W и градиент
на множестве W и градиент 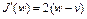 , то необходимое и достаточное условие оптимальности для точки w согласно формуле (5) запишется в виде
, то необходимое и достаточное условие оптимальности для точки w согласно формуле (5) запишется в виде 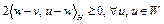 . Отсюда следует неравенство (8).
. Отсюда следует неравенство (8).
Пусть точки  . Тогда из (8) имеем
. Тогда из (8) имеем
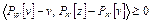 ,
,
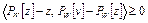 .
.
Суммируя данные неравенства, получим
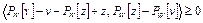 .
.
Отсюда следует
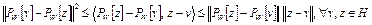 .
.
После деления на 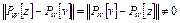 получим неравенство (9). Теорема доказана.
получим неравенство (9). Теорема доказана.
Пример 1. Пусть множество 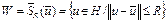 . Пусть точка
. Пусть точка 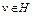 . Используя неравенство (8), можно доказать, что
. Используя неравенство (8), можно доказать, что
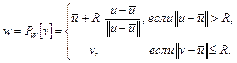 ,
,
Пример 2. Пусть множество 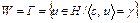 . Пусть точка
. Пусть точка 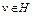 . Тогда
. Тогда
 .
.
Пример 3. Пусть множество 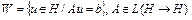 ,
, 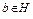 , оператор
, оператор 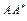 имеет обратный. Пусть точка
имеет обратный. Пусть точка 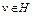 . Тогда
. Тогда
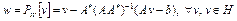 .
.
Пример 4. Пусть множество
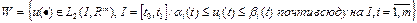 , где
, где 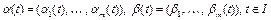 – заданные непрерывные функции. Пусть функция
– заданные непрерывные функции. Пусть функция 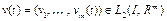 . Тогда
. Тогда
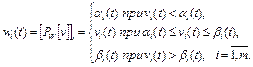
ЛЕКЦИЯ 9.ОТДЕЛИМОСТЬ ВЫПУКЛЫХ МНОЖЕСТВ. ФУНКЦИОНАЛ ЛАГРАНЖА. СЕДЛОВАЯ ТОЧКА
Отделимость выпуклых множеств. Пусть A и B – два множества из банахова пространства X.
Определение 1. Говорят, что гиперплоскость  отделяет множества A и B, если
отделяет множества A и B, если
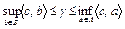 .
.
Если 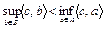 , то множество A и B сильно отделимы. Если
, то множество A и B сильно отделимы. Если 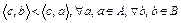 , то множества A и B строго отделимы.
, то множества A и B строго отделимы.
Определение 2. Пусть U – множество из банахова пространства X, точка 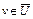 . Гиперплоскость
. Гиперплоскость 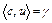 называется опорной к множеству U в точке v, если
называется опорной к множеству U в точке v, если 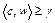 при всех
при всех 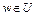 , где
, где 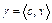 . Иными словами, опорная гиперплоскость разделяет множество U и точку v.
. Иными словами, опорная гиперплоскость разделяет множество U и точку v.
Теорема 1. Пусть U – выпуклое замкнутое множество из гильбертова пространства H, точка 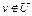 . Тогда множество U и точка v сильно отделимы.
. Тогда множество U и точка v сильно отделимы.
Доказательство. Пусть точка 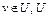 – выпуклое замкнутое множество. Покажем, что множество U и точка v сильно отделимы. Так как выполнены все условия теоремы 6 из лекции 8, то точка
– выпуклое замкнутое множество. Покажем, что множество U и точка v сильно отделимы. Так как выполнены все условия теоремы 6 из лекции 8, то точка 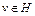 имеет единственную проекцию
имеет единственную проекцию  , причем
, причем
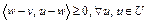 . (1)
. (1)
Пусть элемент 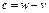 . Рассмотрим скалярное произведение
. Рассмотрим скалярное произведение 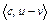 в пространстве H. Из данного скалярного произведения, с учетом (1), получим
в пространстве H. Из данного скалярного произведения, с учетом (1), получим
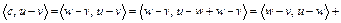
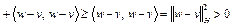 .
.
Следовательно, 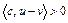 или
или 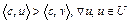 . Это означает, что гиперплоскость
. Это означает, что гиперплоскость 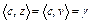 сильно отделяет точку v и множество
сильно отделяет точку v и множество 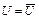 . Теорема доказана.
. Теорема доказана.
Теорема 2. Пусть A и B – два выпуклых множества из гильбертова пространства H, причем 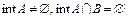 . Тогда существует гиперплоскость
. Тогда существует гиперплоскость 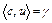 , разделяющая множества A и B, а также их замыкания
, разделяющая множества A и B, а также их замыкания  и
и 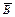 , т.е.
, т.е.
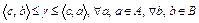 .
.
Если  и
и 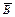 имеют общую граничную точку
имеют общую граничную точку 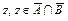 , то
, то 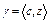 .
.
Доказательство.Пусть множество 
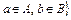 . Можно показать, что множество U выпукло. В самом деле, если
. Можно показать, что множество U выпукло. В самом деле, если 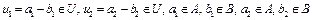 , то точка
, то точка 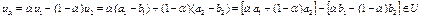 при всех
при всех 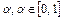 в силу того, что
в силу того, что 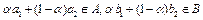 . Итак, множество U выпукло. Так как
. Итак, множество U выпукло. Так как 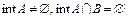 , то элемент
, то элемент 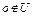 . Аналогичным путем, как в доказательстве теоремы 1, можно показать, что существует гиперплоскость
. Аналогичным путем, как в доказательстве теоремы 1, можно показать, что существует гиперплоскость 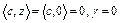 , отделяющая множество U и элемент
, отделяющая множество U и элемент 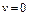 . Следовательно,
. Следовательно, 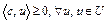 . Тогда
. Тогда 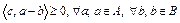 . Отсюда имеем
. Отсюда имеем 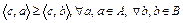 . Это означает, что множества A и B отделимы,
. Это означает, что множества A и B отделимы, 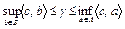 .
.
Покажем, что гиперплоскость 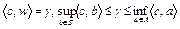 отделяет замыкания
отделяет замыкания  и
и 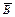 . Действительно, пусть
. Действительно, пусть 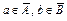 – предельные точки множеств A и B соответственно. Тогда существуют последовательности
– предельные точки множеств A и B соответственно. Тогда существуют последовательности 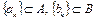 такие, что
такие, что 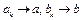 при
при  . По вышедоказанному,
. По вышедоказанному, 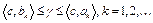 . Отсюда при
. Отсюда при  получим
получим 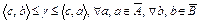 . Следовательно, множества
. Следовательно, множества  и
и 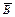 отделимы. Если точка
отделимы. Если точка  , то при
, то при  получим
получим 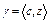 . Теорема доказана.
. Теорема доказана.
Можно доказать, что утверждения теорем 1, 2 верны в любом банаховом пространстве X.
Функционал Лагранжа. Седловая точка. Рассмотрим следующую задачу оптимального управления
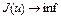 , (2)
, (2)
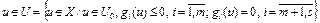 , (3) где
, (3) где 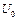 – заданное множество из банахова пространства X,
– заданное множество из банахова пространства X, 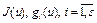 – заданные функционалы на множестве
– заданные функционалы на множестве 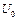 . Множество
. Множество
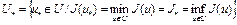 , где
, где 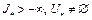 .
.
Определение 3. Функционал
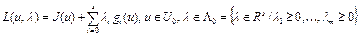 . (4) называется функционалом Лагранжа для задачи (2), (3),
. (4) называется функционалом Лагранжа для задачи (2), (3), 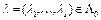 – множители Лагранжа.
– множители Лагранжа.
Определение 4. Пара 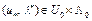 называется седловой точкой функционала Лагранжа (4), если
называется седловой точкой функционала Лагранжа (4), если
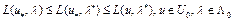 . (5)
. (5)
Лемма 1. Для того, чтобы пара 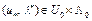 была седловой точкой функционала Лагранжа (4), необходимо и достаточно выполнение следующих условий:
была седловой точкой функционала Лагранжа (4), необходимо и достаточно выполнение следующих условий:
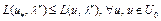 , (6)
, (6)
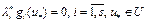 . (7)
. (7)
Доказательство. Необходимость. Пусть пара 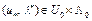 – седловая точка. Покажем, что выполнены условия (6), (7). Из определения седловой точки следует, что выполнено неравенство (5). Тогда из правого неравенства следует условие (6). Левое неравенство из (5) запишется в виде
– седловая точка. Покажем, что выполнены условия (6), (7). Из определения седловой точки следует, что выполнено неравенство (5). Тогда из правого неравенства следует условие (6). Левое неравенство из (5) запишется в виде
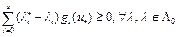 . (8)
. (8)
Заметим, что:
а) вектор
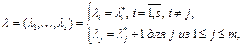 (9) принадлежит множеству
(9) принадлежит множеству 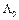 . Подставляя значение
. Подставляя значение 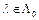 из (9) в неравенство (8), имеем
из (9) в неравенство (8), имеем 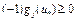 . Отсюда следует, что
. Отсюда следует, что 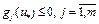 .
.
б) аналогично, вектор
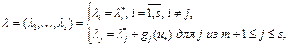
также принадлежит множеству 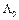 . Подставляя значение
. Подставляя значение 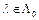 из (8), получим
из (8), получим 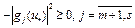 . Следовательно,
. Следовательно, 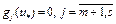 . Из а) и б) следует, что
. Из а) и б) следует, что 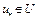 .
.
в) пусть вектор 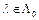 определяется так
определяется так
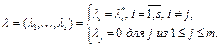
Для данного 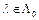 из (8) следует, что
из (8) следует, что 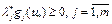 . Так как значение
. Так как значение 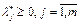 , по доказанному выше значение
, по доказанному выше значение 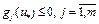 , следовательно, имеет место равенство
, следовательно, имеет место равенство 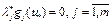 . Из
. Из 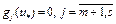 следует, что
следует, что 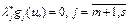 . Итак,
. Итак, 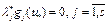 . Необходимость доказана.
. Необходимость доказана.
Достаточность. Пусть выполнены условия (6), (7). Покажем, что пара 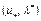 – седловая точка функционала Лагранжа (4). Легко убедиться в том, что
– седловая точка функционала Лагранжа (4). Легко убедиться в том, что  . В самом деле, если
. В самом деле, если 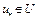 , то
, то 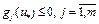 . Из (7) следует, что
. Из (7) следует, что 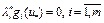 . Так как
. Так как 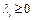 , то
, то 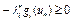 . Тогда сумма
. Тогда сумма
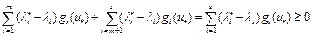 ,
,
так как 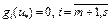 . Отсюда следует, что
. Отсюда следует, что 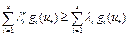 . Тогда
. Тогда
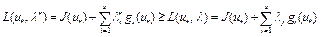 . (10)
. (10)
Из (6) и (10) получим 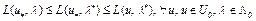 . Это означает, что пара
. Это означает, что пара 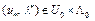 – седловая точка функционала Лагранжа (4). Теорема доказана.
– седловая точка функционала Лагранжа (4). Теорема доказана.
Теорема 3. Если пара 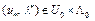 – седловая точка функционала Лагранжа (4), то
– седловая точка функционала Лагранжа (4), то 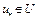 является решением задачи (2), (3), т.е.
является решением задачи (2), (3), т.е. 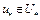 .
.
Доказательство. Как следует из леммы 1, для пары 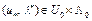 выполнены соотношения (6), (7). Тогда значение
выполнены соотношения (6), (7). Тогда значение 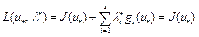 , так как точка
, так как точка 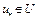 . Теперь неравенство (6) запишется так:
. Теперь неравенство (6) запишется так:
 . (11)
. (11)
Поскольку множество 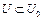 , то неравенство (11), в частности, верно для любого
, то неравенство (11), в частности, верно для любого 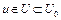 , т.е.
, т.е.
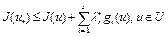 . (12)
. (12)
Как следует из условия (3), если 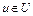 , то
, то 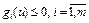 , и
, и 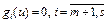 . Следовательно, произведение
. Следовательно, произведение 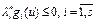 , где
, где 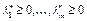 . Тогда из (12) следует, что
. Тогда из (12) следует, что 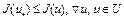 . Это означает, что
. Это означает, что 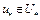 . Теорема доказана.
. Теорема доказана.
Существование седловой точки.Рассмотрим следующую задачу выпуклого программирования
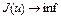 , (13)
, (13)
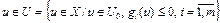 . (14)
. (14)
Следующая теорема дает достаточное условие существования седловой точки функционала Лагранжа
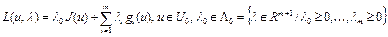 (15) для задачи (13), (14).
(15) для задачи (13), (14).
Теорема 4. Если 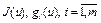 – выпуклые функционалы, определенные на выпуклом множестве
– выпуклые функционалы, определенные на выпуклом множестве 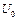 , множество U регулярно, т.е. существует точка
, множество U регулярно, т.е. существует точка 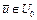 такая, что
такая, что  , то для каждой точки
, то для каждой точки 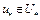 необходимо существуют множители Лагранжа
необходимо существуют множители Лагранжа 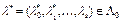 такие, что пара
такие, что пара 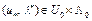 образует седловую точку функционала Лагранжа (15).
образует седловую точку функционала Лагранжа (15).
Доказательство. Рассмотрим множества
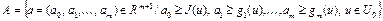 , (16)
, (16)
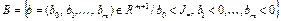 . (17)
. (17)
Легко убедиться в том, что: 1) 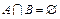 ; 2) A, B – выпуклые множества; 3) множества А и В отделимы (см. теорему 2), т.е. существует гиперплоскость
; 2) A, B – выпуклые множества; 3) множества А и В отделимы (см. теорему 2), т.е. существует гиперплоскость 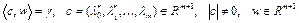 , разделяющая множества А и В, а также их замыкания
, разделяющая множества А и В, а также их замыкания 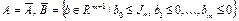 . Следовательно, выполняются неравенства
. Следовательно, выполняются неравенства
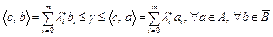 . (18)
. (18)
Заметим, что если точка 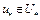 , то
, то 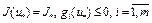 . Следовательно, вектор
. Следовательно, вектор 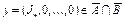 , величина
, величина 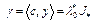 . Теперь неравенство (18) запишется в виде
. Теперь неравенство (18) запишется в виде
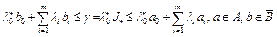 . (19)
. (19)
Тогда, если:
а) выберем 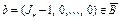 . Тогда из левого неравенства (19) имеем
. Тогда из левого неравенства (19) имеем 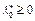 ;
;
б) выберем 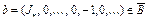 . Тогда из левого неравенства (19) получим
. Тогда из левого неравенства (19) получим 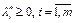 ;
;
в) точка 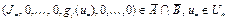 . Из (19) имеем
. Из (19) имеем 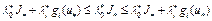 . Тогда
. Тогда 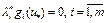 ;
;
г) поскольку множество U регулярно, то существует точка 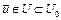 такая, что
такая, что 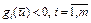 . Точка
. Точка 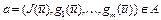 . Тогда из (19) имеем
. Тогда из (19) имеем 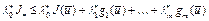 . Отсюда следует, что если
. Отсюда следует, что если 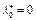 , то, хотя бы для одного i, имеем
, то, хотя бы для одного i, имеем 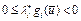 , вектор
, вектор 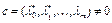 . Это невозможно. Следовательно,
. Это невозможно. Следовательно, 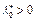 . Полагаем
. Полагаем 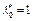 .
.
д) пусть 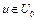 . Тогда
. Тогда 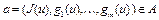 . Из правого неравенства (19) получаем
. Из правого неравенства (19) получаем 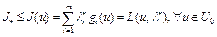 . Так как произведение
. Так как произведение 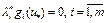 , то
, то
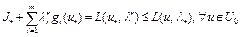 . (20)
. (20)
Из (20) и  следует, что пара
следует, что пара 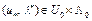 – седловая точка функционала Лагранжа (15). Теорема доказана.
– седловая точка функционала Лагранжа (15). Теорема доказана.
Необходимые условия оптимальности. Пусть X, Y – банаховы пространства, 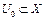 – некоторое множество, оператор
– некоторое множество, оператор 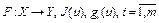 – функционалы, определенные на
– функционалы, определенные на 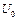 . Рассмотрим следующую задачу оптимального управления:
. Рассмотрим следующую задачу оптимального управления:
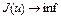 , (21)
, (21)
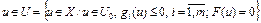 . (22)
. (22)
Для задачи (21), (22) функционал Лагранжа имеет вид
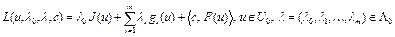 , где
, где 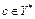 .
.
Теорема 5. Пусть 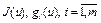 – выпуклые функционалы, определенные на выпуклом множестве
– выпуклые функционалы, определенные на выпуклом множестве 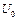 банахова пространства X, оператор
банахова пространства X, оператор  ,
, 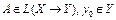 . Тогда для любой точки
. Тогда для любой точки 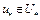 существуют не равные одновременно нулю множители Лагранжа
существуют не равные одновременно нулю множители Лагранжа 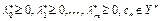 такие, что
такие, что
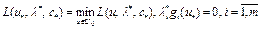 . (23)
. (23)
Если, кроме того, 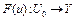 – образ множества
– образ множества 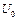 , равный
, равный 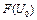 , содержит окрестность нуля пространства Y и существует точка
, содержит окрестность нуля пространства Y и существует точка 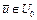 такая, что
такая, что 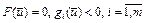 , то
, то 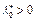 . В этом случае условия (23) являются и достаточными для того, чтобы
. В этом случае условия (23) являются и достаточными для того, чтобы 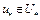 .
.
Дата добавления: 2015-08-21; просмотров: 1410;
