Глава 7. Краевые задачи оптимального управления………………..226 1 страница
Лекция 31. Краевые задачи оптимального управления линейных
систем с линейными функционалами I……………………...226
Лекция 32. Краевые задачи оптимального управления линейных
систем с линейными функционалами II…….……………….233
Лекция 33. Краевые задачи оптимального управления линейных
квадратичным функционалом без ограничений……………243
Лекция 34. Краевые задачи оптимального управления
нелинейных систем I………………………………………….252
Лекция 35. Краевые задачи оптимального управления
нелинейных систем II……..…………………………………..260
Лекция 36. Краевые задачи оптимального управления
нелинейных систем III……..………………………………….268
ЛИТЕРАТУРА ……………………………………………………………278
ПРЕДИСЛОВИЕ
Книга написана на основе лекций, прочитанных автором в последние годы на механико-математическом факультете КазНУ им. аль‑Фараби, а также научных работ автора по оптимальному управлению.
Она состоит из двух частей. В первой изложены основы теории оптимального управления, а во второй части приведены теория и методы решения краевых задач оптимального управления. Результаты первой части содержатся в главах I – IV, вторая часть содержит главы V – VII и написана на основе научных результатов автора.
Наиболее крупными достижениями научно-технического прогресса XX века называют: расщепление атома, освоение космоса, создание электронно-вычислительной техники. Управление ядерными реакторами, летательными аппаратами, сложными технологическими процессами, исследование задач экономики требовали создания нового направления в математике – теории оптимального управления. Бурное развитие электронно-вычислительной техники, появление компьютеров нового поколения открывают путь для решения сложных задач оптимального управления.
Возникает необходимость подготовки математиков по новому направлению – математической теории управления. Современная теория управления имеет следующие разделы: математическое программирование, теория оптимального управления, численные методы решения экстремальных задач.
Данная книга является продолжением книги автора “Лекции по методам оптимизации”, изданной в 1996 году, в которой излагались теория и методы решения задач минимизации в конечномерных пространствах, вариационное исчисление, принцип максимума и динамическое программирование в задачах оптимального управлениями процессами, описываемыми обыкновенными дифференциальными уравнениями.
Следует отметить, что условия оптимальности в форме принципа максимума Понтрягина и принцип динамического программирования Беллмана не конструктивны для решения прикладных задач, имеющих разрыв между теоретическими исследованиями задач оптимизации и практикой их решения. На практике в основном используют различные методы направленного перебора, разностные или градиентные методы спуска, не связанные принципом максимума и принципом динамического программирования.
Формулировка условий оптимальности в форме, удобной для построения минимизирующей последовательности, доказательство их сходимости и получение оценок сходимости являются актуальными проблемами теории оптимального управления.
В данной книге сделана попытка рассмотрения на основе единого подхода условий оптимальности и конструктивных методов построения оптимального решения краевых задач оптимального управления с фазовыми и интегральными ограничениями.
В главе I (лекции 1 – 5) излагаются задачи оптимального управления, основные определения, основы дифференциального исчисления в банаховом пространстве, теоремы существования и единственности решения для дифференциального уравнения, итерационный процесс Ньютона-Канторовича, теорема Вейерштрасса в банаховом пространстве.
В главе II (лекции 6 – 10) приведены сведения из выпуклого анализа, применимые к задачам оптимального управления: выпуклые множества и их свойства, выпуклые функционалы и их свойства, теорема о глобальном минимуме, условия оптимальности, проекция точки на множество, основы теории отделимости выпуклых множеств, метод множителей Лагранжа, теоремы о существовании седловой точки, достаточные условия слабой бикомпактности выпуклых множеств, слабой полунепрерывности снизу выпуклых функционалов изложены в виде пяти лекций с названием “Выпуклый анализ в банаховом пространстве”.
В главе III (лекции 11 – 15) рассматриваются градиенты функционалов, определенных на множестве решений обыкновенных дифференциальных уравнений, параболического уравнения, гиперболического уравнения. Множество решений порождено управляющими воздействиями из заданных множеств и гильбертовых пространств. Приведены алгоритмы определения градиентов для соответствующих функционалов, условия Липшица для градиентов функционалов, а также условия оптимальности для различных задач оптимального управления.
В главе IV (лекции 16 – 20) изложены методы минимизации функционалов в банаховом пространстве: градиентный метод, метод проекции градиента, метод условного градиента, метод сопряженных направлений, метод Ньютона, метод штрафных функционалов. Приведены алгоритмы и основные теоремы о минимизирующих последовательностях и оценки их сходимости, примеры.
Результаты глав I – IV содержатся в двадцати лекциях и они позволяют решать задачи оптимального управления со свободным правым концом траектории для обыкновенных дифференциальных уравнений. Применение этих результатов для решения краевых задач оптимального управления с фазовыми и интегральными ограничениями затруднительно и неконструктивно. Решение краевых задач оптимального управления с ограничениями требует иных подходов. Один из подходов решения краевых задач оптимального управления приведен в главах V – VII.
Глава V (лекции 21 – 25) посвящена проблеме управляемости динамических систем и линейным интегральным уравнениям. Решения ряда краевых задач управляемости и оптимального управления, классических краевых задач, задачи на собственные значения и предельных циклов могут быть сведены к решению интегральных уравнений. Получены необходимые и достаточные условия существования решения линейных интегральных уравнений. Найдены общие решения линейных интегральных уравнений. Результаты данной главы являются основой для решения краевых задач оптимального управления.
В главе VI (лекции 26 – 30) изложены методы решения задачи оптимального быстродействия линейных и нелинейных систем при наличии фазовых и интегральных ограничений, а также ограничения на значения управления. Предлагается принцип погружения, который позволяет свести исходную задачу оптимального быстродействия к специфической задаче оптимального управления процессов со свободными правыми концами траектории. Получены необходимое и достаточное условия разрешимости задачи быстродействия и разработан конструктивный метод построения решения задачи оптимального быстродействия.
В главе VII (лекции 31 – 36) приведены решения краевых задач оптимального управления линейных систем с линейными и квадратичными функционалами, а также нелинейных систем, когда имеются фазовые, интегральные ограничения и ограничения на значения управления с функционалом общего вида. Решены следующие три задачи: существования решения, построения допустимого управления, построения оптимального решения путем сужения области допустимого управления.
Книга предназначена прежде всего для студентов старших курсов университетов, для полного понимания всех частей книги нужно владеть университетским курсом функционального анализа. Однако следует отметить, что отсутствие знаний по функциональному анализу не будет препятствовать пониманию материалов книги, если читатель готов принимать ряд утверждений не в самой общей их форме, а в контексте данного рода.
Теория оптимального управления относится к одной из наиболее быстро развивающихся областей математики, поэтому создать учебник, который будет обладать завершенностью и не иметь каких-либо недостатков, очень затруднительно.
Автор благодарен коллективу кафедры теории управления механико‑математического факультета КазНУ им. аль-Фараби, доценту Белогурову А.П. за оказанную помощь в подготовке рукописи к изданию, будет признателен всем, кто пришлет свои замечания и отзывы по данной книге.
Айсагалиев С.А.
ГЛАВА 1.ВВЕДЕНИЕ В ТЕОРИЮ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
Для решения актуальных проблем естественных наук, техники, экономики, экологии и др. необходимы новые математические методы, позволяющие решать сложные научно-технические задачи. В частности, математические модели процессов управления ядерными и химическими реакторами, управления электроэнергетическими и робототехническими системами, управление экономикой и экологией, управление движением летательных аппаратов и искусственных спутников и др. являются сложными краевыми задачами оптимального управления.
Современные конкурентоспособные системы должны проектироваться с учетом нескольких требований на их динамические свойства. Основное требование, определяемое назначением системы, называется критерием качества. Математическая формализация задачи выбора оптимальных параметров системы чаще всего приводит к постановке задачи нахождения таких значений параметров, при которых целевой функционал (критерий качества) достигает своей нижней либо верхней грани на некотором множестве допустимых значений параметров. При этом множество допустимых значений параметров определяется другими требованиями на динамику системы, которые формализуются в виде интегральных ограничений. Каждая система функционирует нормально в заданной рабочей зоне. Как правило, уравнение движения системы адекватно отражает реальные процессы в рабочей зоне системы. В математических моделях систем рабочая зона задается в виде фазовых ограничений на состояние системы. Ограниченность ресурсов математически формализуется в виде ограничения на значения управления, а функциональные свойства допустимых управлений определяют класс функций управления. Граничные условия определяют начальное и конечное состояние системы, которые, как правило, являются элементами заданных множеств, определяемых неравенствами и равенствами.
ЛЕКЦИЯ 1.ПОСТАНОВКА ЗАДАЧИ. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Математическая формулировка задачи оптимального управления имеет следующий вид: минимизировать функционал
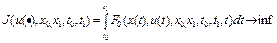 (1)
(1)
на множестве решений дифференциального уравнения
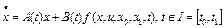 , (2)
, (2)
 , (3)
, (3)
с краевыми условиями
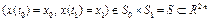 , (4)
, (4)
при наличии фазовых ограничений
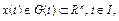 (5)
(5)
а также интегральных ограничений
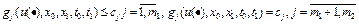 , (6)
, (6)
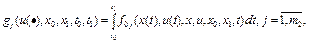 (7)
(7)
ограничения на значения уравнения
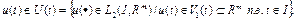 . (8)
. (8)
Здесь 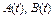 – матрицы с кусочно–непрерывными элементами
– матрицы с кусочно–непрерывными элементами 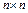 ,
, 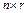 (в частности
(в частности 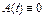 ,
, 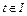 ), вектор функция
), вектор функция 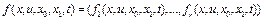 непрерывна по совокупности переменных
непрерывна по совокупности переменных 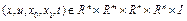 , вектор функция
, вектор функция  и скалярная функция
и скалярная функция 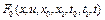 определены и непрерывны по совокупности переменных, S–заданное ограниченное выпуклое множество из
определены и непрерывны по совокупности переменных, S–заданное ограниченное выпуклое множество из 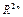 , U=U(t),
, U=U(t), 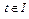 –заданное ограниченное выпуклое замкнутое множество из
–заданное ограниченное выпуклое замкнутое множество из  , G(t),
, G(t), 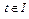 – заданное ограниченное выпуклое замкнутое множество из
– заданное ограниченное выпуклое замкнутое множество из 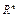 ,
, 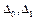 – заданные отрезки из
– заданные отрезки из 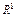 .
.
Можно привести множество примеров прикладных задач, которые сводятся к решению задач (1)–(8).
Пример 1. Ракета запускается из области S0 для поражения цели, находящейся в области S1. Уравнение движения ракеты в первом приближении имеет вид (2), где  – изменение тяговой силы реактивного двигателя ограниченной мощности. Разрешенный воздушный коридор для ракеты определяется множеством G(t),
– изменение тяговой силы реактивного двигателя ограниченной мощности. Разрешенный воздушный коридор для ракеты определяется множеством G(t), 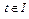 . Необходимо найти точку запуска ракеты
. Необходимо найти точку запуска ракеты 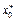 из множества S0 и закон изменения тяговой силы
из множества S0 и закон изменения тяговой силы 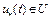 такие, чтобы ракета попала в точку
такие, чтобы ракета попала в точку 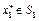 и при этом траектория ракеты не покидала заданный воздушный коридор G(t),
и при этом траектория ракеты не покидала заданный воздушный коридор G(t), 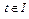 , расход топлива был минимальным (значение функционала (1)).
, расход топлива был минимальным (значение функционала (1)).
Пример 2. Пусть экономика страны в момент времени t0 находится в состоянии 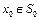 . Для того, чтобы создать рыночную экономику, необходимо перевести экономику в состояние
. Для того, чтобы создать рыночную экономику, необходимо перевести экономику в состояние 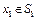 . В данном случае уравнение (2) описывает изменение валового выпуска продукции отраслей экономики, а компонентами вектора управления являются: инвестиции, основные фонды, трудовые ресурсы, потребление. Для того, чтобы не было нехватки продукции или перепроизводства, величина валового выпуска продукции должна находиться в заданной области G(t),
. В данном случае уравнение (2) описывает изменение валового выпуска продукции отраслей экономики, а компонентами вектора управления являются: инвестиции, основные фонды, трудовые ресурсы, потребление. Для того, чтобы не было нехватки продукции или перепроизводства, величина валового выпуска продукции должна находиться в заданной области G(t), 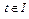 .
.
Необходимо найти закон изменения инвестиций, основных фондов, трудовых ресурсов и потребления, при котором экономика страны в момент времени t1 перешла бы в состояние 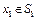 и блага от потребления были максимальны (значение функционала).
и блага от потребления были максимальны (значение функционала).
Пример 3. Рассмотрим энергетическую систему, состоящую из сети и нескольких генераторов, работающих в синхронном режиме. Пусть в момент времени t0 из-за коротких замыканий либо перегрузки сети генераторы вышли из синхронного режима и их состояние определяется вектором 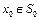 . В заданном случае уравнение (2) соответствует уравнению движения синхронных генераторов, управление
. В заданном случае уравнение (2) соответствует уравнению движения синхронных генераторов, управление 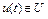 – давление и температура пара. Необходимо привести систему в состояние синхронного режима работы генераторов, определяемое вектором
– давление и температура пара. Необходимо привести систему в состояние синхронного режима работы генераторов, определяемое вектором 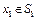 .
.
При этом изменения напряжения и тока в сети должны находиться в заданных пределах G(t), 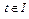 . Необходимо найти закон изменения давления и температуры пара в управляемых генераторах, обеспечивающий состояние x1 в момент времени t1 с минимальной потерей электроэнергии в переходном режиме (значение функционала).
. Необходимо найти закон изменения давления и температуры пара в управляемых генераторах, обеспечивающий состояние x1 в момент времени t1 с минимальной потерей электроэнергии в переходном режиме (значение функционала).
Заметим, что в прикладных задачах часто встречаются следующие множества:
1) вектор 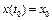 – начальное состояние системы,
– начальное состояние системы,  – состояние системы в момент времени t1, пара (
– состояние системы в момент времени t1, пара ( 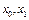 )
) 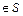 , множество S определяется одним из следующих условий:
, множество S определяется одним из следующих условий:
а) 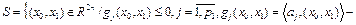
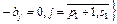
б) 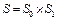 :
:
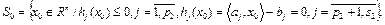

где 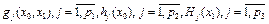 – выпуклые функции.
– выпуклые функции.
2) множество G(t) определяется одним из следующих уравнений:
а) 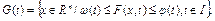 где
где 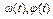 – заданные s-мерные вектор функции,
– заданные s-мерные вектор функции, 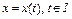 – решение дифференциального уравнения (2);
– решение дифференциального уравнения (2);
б)
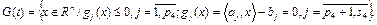 где
где 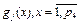 – выпуклые функции,
– выпуклые функции, 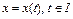 .
.
3) Множество U определяется одним из следующих условий:
а) 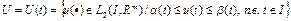 , где
, где 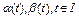 – заданные m–мерные вектор функции;
– заданные m–мерные вектор функции;
б) 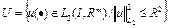 , где R>0– заданное число.
, где R>0– заданное число.
Определение 1. Вектор управления 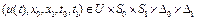 – называется допустимым управлением для задачи (1) – (8), если краевая задача (2) – (8) имеет решение. Множество всех допустимых управлений обозначим через W, где
– называется допустимым управлением для задачи (1) – (8), если краевая задача (2) – (8) имеет решение. Множество всех допустимых управлений обозначим через W, где 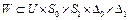 . Элементы множества W обозначим через
. Элементы множества W обозначим через  .
.
Из данного определения следует, что для каждого элемента множества W выполняются: 1) решение 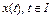 дифференциального уравнения (2), исходящее из точки
дифференциального уравнения (2), исходящее из точки 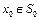 , удовлетворяет условию
, удовлетворяет условию 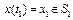 , причем
, причем 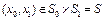 ; 2) выполнено включение
; 2) выполнено включение 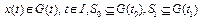 ; 3) для каждого элемента множества W выполнены:
; 3) для каждого элемента множества W выполнены: 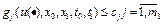 ;
; 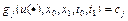 ,
, 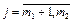 .
.
Задача 1. Найти необходимые и достаточные условия существования решения задачи оптимального управления (1) – (8).
Заметим, что задача оптимального управления (1) – (8) имеет решение тогда и только тогда, когда краевая задача (2) – (8) имеет решение.
Задача 2. Найти допустимое управление 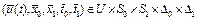 , где
, где 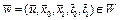 .
.
Если задача 1 имеет решение, то существует допустимое управление.
Задачу 1 часто называют задачей управляемости, а задачу 2 – решением задачи управляемости.
Пусть множество 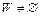 , где
, где 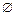 – пустое множество. В этом случае задача оптимального управления (1) – (8) может быть представлена в виде
– пустое множество. В этом случае задача оптимального управления (1) – (8) может быть представлена в виде
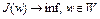 . (9)
. (9)
Определение 2. Элемент  называется оптимальным управлением для задачи (1) – (8), если выполняется неравенство
называется оптимальным управлением для задачи (1) – (8), если выполняется неравенство  при всех
при всех  . Величина
. Величина 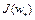 называется наименьшим или минимальным значением функционала
называется наименьшим или минимальным значением функционала 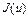 на множестве W. Множество
на множестве W. Множество 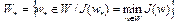 содержит все оптимальные управления для задачи (1) – (8).
содержит все оптимальные управления для задачи (1) – (8).
Определение 3. Говорят, что функционал  ограничен снизу на множестве W, если существует число M такое, что
ограничен снизу на множестве W, если существует число M такое, что 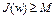 при всех
при всех  . Функционал
. Функционал  не ограничен снизу на множестве W, если существует последовательность
не ограничен снизу на множестве W, если существует последовательность 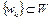 , такая, что
, такая, что 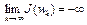 .
.
Определение 4. Пусть функционал  ограничен снизу на множестве W. Тогда величина
ограничен снизу на множестве W. Тогда величина 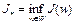 называется нижней гранью функционала
называется нижней гранью функционала  на множестве W, если: 1)
на множестве W, если: 1) 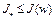 при всех
при всех  ; 2) для любого сколь угодно малого числа
; 2) для любого сколь угодно малого числа 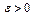 найдется точка
найдется точка 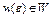 , такая, что значение
, такая, что значение 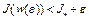 . В случае, когда функционал
. В случае, когда функционал  не ограничен снизу на множестве W, нижняя грань
не ограничен снизу на множестве W, нижняя грань 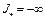 .
.
Если множество  , то
, то 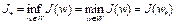 , т.е. нижняя грань функционала
, т.е. нижняя грань функционала  на W достигается. Нижняя грань
на W достигается. Нижняя грань 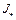 всегда существует, а
всегда существует, а  – не всегда.
– не всегда.
Определение 5. Последовательность 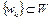 называется минимизирующей для функционала
называется минимизирующей для функционала  , определенного на множестве W, если предел
, определенного на множестве W, если предел 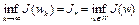 .
.
Как следует из определения нижней грани, в случае  имеем последовательность
имеем последовательность 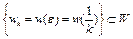 , для которой
, для которой 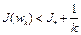 . Отсюда следует, что предел
. Отсюда следует, что предел 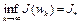 . Таким образом, минимизирующая последовательность
. Таким образом, минимизирующая последовательность 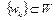 всегда существует.
всегда существует.
Определение 6. Говорят, что последовательность 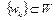 сходится к множеству
сходится к множеству 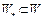 , если предел
, если предел  , где
, где 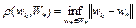 – расстояние от точки
– расстояние от точки 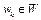 до множества
до множества 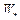 .
.
Следует отметить, что если множество  , то всегда существует минимизирующая последовательность, которая сходится к множеству
, то всегда существует минимизирующая последовательность, которая сходится к множеству 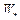 . Однако утверждение о том, что любая минимизирующая последовательность сходится к множеству
. Однако утверждение о том, что любая минимизирующая последовательность сходится к множеству 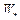 , в общем случае неверно.
, в общем случае неверно.
Определение 7. Точки  называют точками абсолютного или глобального минимума функционала
называют точками абсолютного или глобального минимума функционала  на множестве W. Точка
на множестве W. Точка  называется точкой локального минимума, если существует число
называется точкой локального минимума, если существует число 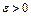 такое, что
такое, что 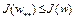 при всех
при всех 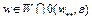 , где
, где 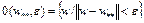 .
.
Если при некотором 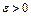 верно неравенство
верно неравенство 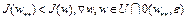 , то
, то 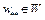 называется точкой строгого локального минимума.
называется точкой строгого локального минимума.
Пусть имеются решения задач 1,2. Тогда задача оптимального управления имеет вид (9) и является корректным решением следующих задач.
Задача 3. Найти величину 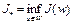 . В этом случае, независимо от того, будет ли множество
. В этом случае, независимо от того, будет ли множество 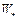 пусто или непусто, задача (9) имеет решение.
пусто или непусто, задача (9) имеет решение.
Задача 4. Найти величину 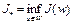 и точку
и точку  . В этом случае, для того чтобы задача (9) имела решение, необходимо, чтобы множество
. В этом случае, для того чтобы задача (9) имела решение, необходимо, чтобы множество  .
.
Задача 5. Найти минимизирующую последовательность 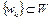 , где
, где 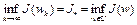 . В этом случае задача (9) всегда имеет решение.
. В этом случае задача (9) всегда имеет решение.
Задача 6. Найти минимизирующую последовательность 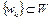 , которая сходится к множеству
, которая сходится к множеству 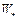 . В данном случае необходимо, чтобы множество
. В данном случае необходимо, чтобы множество 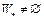 .
.
Наиболее часто на практике требуется решение задач 4,6 (см. примеры 1–3).
ЛЕКЦИЯ 2.ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ В БАНАХОВОМ ПРОСТРАНСТВЕ
Основные понятия линейного функционала и линейного оператора были изучены в курсе функционального анализа. Для изучения теории оптимального управления требуются некоторые сведения о нелинейных функционалах и нелинейных операторах в бесконечномерных пространствах. Ниже приведены основы дифференциального исчисления в банаховом пространстве.
Дифференцирование нелинейных операторов. Пусть X, Y – два банаховых пространства, F(x) – нелинейный оператор с областью определения 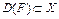 и со значениями в
и со значениями в 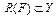 . Пусть оператор F(x) определен в S–окрестности точки
. Пусть оператор F(x) определен в S–окрестности точки 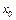 , где
, где 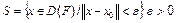 .
.
Дата добавления: 2015-08-21; просмотров: 2339;
