Критерий Римана интегрируемости функции
Лекция 16. Классы интегрируемых функций
План
Критерий Римана интегрируемости функции
Достаточные условия интегрируемости функции по Риману
Свойства определенного интеграла
Интеграл с переменным верхним пределом
Критерий Римана интегрируемости функции
Теорема 1 (критерий Римана интегрируемости функции). Для того, чтобы функция  была интегрируема по Риману на сегменте
была интегрируема по Риману на сегменте  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
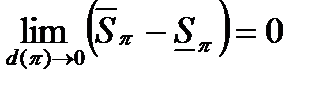 .
.
Пример. Рассмотрим функцию Дирихле:
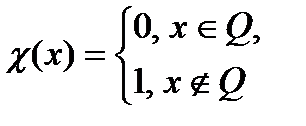 .
.
Докажем, что 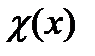 не интегрируема по Риману на любом сегменте
не интегрируема по Риману на любом сегменте  . Возьмем любое разбиение
. Возьмем любое разбиение 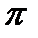 сегмента
сегмента  . Понятно, что всегда
. Понятно, что всегда
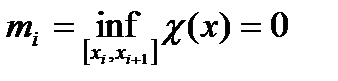 ,
, 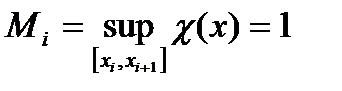 .
.
Тогда любая
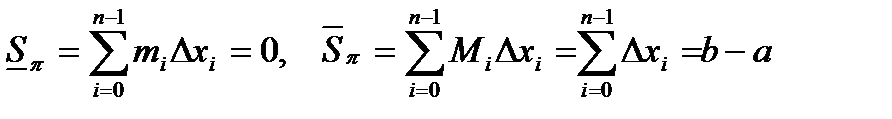 ,
,
а 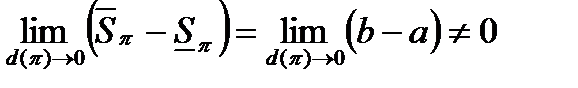 .
.
Таким образом, функция 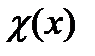 не интегрируема по Риману на любом сегменте
не интегрируема по Риману на любом сегменте  .
.
Замечание. Если  интегрируема на
интегрируема на  , то не только интегральные суммы, но и суммы Дарбу стремятся к значению интеграла при
, то не только интегральные суммы, но и суммы Дарбу стремятся к значению интеграла при 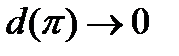 .
.
Обозначим 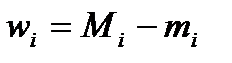 - колебание функции на частичном сегменте
- колебание функции на частичном сегменте 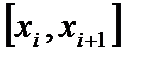 . В этих обозначениях
. В этих обозначениях
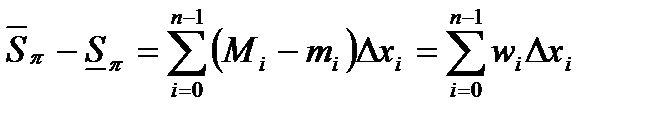 .
.
Тогда критерий Римана интегрируемости функции может быть сформулирован следующим образом: для того, чтобы функция  была интегрируема по Риману на сегменте
была интегрируема по Риману на сегменте  необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
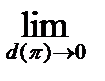
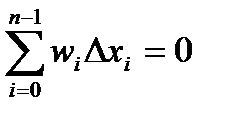 .
.
Дата добавления: 2015-08-21; просмотров: 2717;
