Свойства определенного интеграла
1. Пусть функция  интегрируема по Риману на сегменте
интегрируема по Риману на сегменте  (тогда она обязательно будет ограниченной на этом сегменте). Если изменить значение функции в конечном количестве точек, то получим интегрируемую по Риману функцию
(тогда она обязательно будет ограниченной на этом сегменте). Если изменить значение функции в конечном количестве точек, то получим интегрируемую по Риману функцию 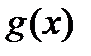 , к тому же
, к тому же
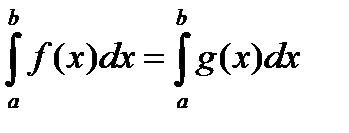 .
.
Доказательство. Возьмем любое разбиение сегмента  :
:
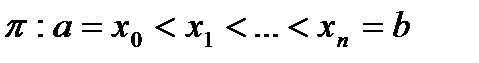 .
.
Построим интегральные суммы для функций  и
и 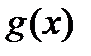 , которые отвечают разбиению
, которые отвечают разбиению 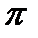 :
:
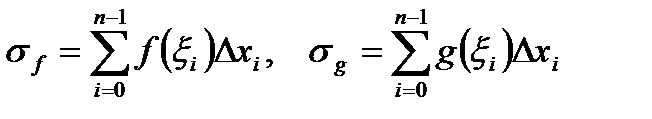 ,
,
точки 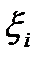 берем произвольно на частичных сегментах
берем произвольно на частичных сегментах 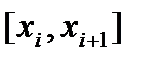 , но одинаковыми для обеих функций
, но одинаковыми для обеих функций  и
и 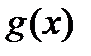 . Интегральные суммы
. Интегральные суммы 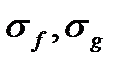 могут отличаться одна от другой лишь на конечное количество слагаемых (
могут отличаться одна от другой лишь на конечное количество слагаемых ( 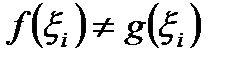 только тогда, когда точка
только тогда, когда точка 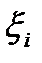 - это та точка, в которой было изменено значение функции
- это та точка, в которой было изменено значение функции  , а таких точек лишь конечное количество). Каждое из слагаемых в интегральных суммах
, а таких точек лишь конечное количество). Каждое из слагаемых в интегральных суммах 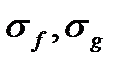 стремится к 0, когда
стремится к 0, когда 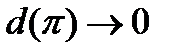 , а потому будут стремиться к нулю и те слагаемые (их конечное количество), которыми отличаются
, а потому будут стремиться к нулю и те слагаемые (их конечное количество), которыми отличаются 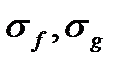 . Поскольку по условию функция
. Поскольку по условию функция  интегрируема по Риману на сегменте
интегрируема по Риману на сегменте  , это по определению существует
, это по определению существует
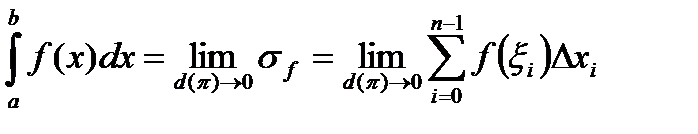 .
.
Поскольку из вышесказанного вытекает, что
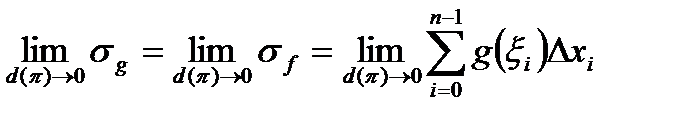 ,
,
т.е., благодаря существованию предела 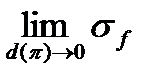 функция
функция 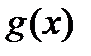 также буде интегрируемой по Риману, а благодаря равенству пределов
также буде интегрируемой по Риману, а благодаря равенству пределов 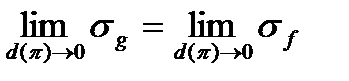 получим, что
получим, что
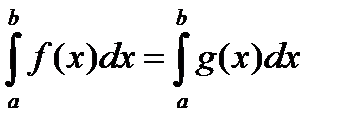 .
.
Задание. Пусть функция 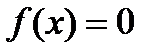 на
на 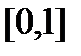 за исключением конечной совокупности точек, где функция принимает значение 1. Будет ли
за исключением конечной совокупности точек, где функция принимает значение 1. Будет ли 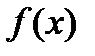 интегрируема по Риману на
интегрируема по Риману на 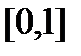 ? Если она интегрируема по Риману, то чему равен ее интеграл? Ответ объяснить.
? Если она интегрируема по Риману, то чему равен ее интеграл? Ответ объяснить.
2. Пусть функция  интегрируема по Риману на сегменте
интегрируема по Риману на сегменте  , а
, а 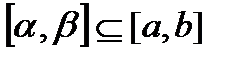 . Тогда
. Тогда  интегрируема по Риману на сегменте
интегрируема по Риману на сегменте 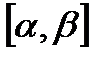 .
.
Доказательство. Поскольку  интегрируема по Риману на сегменте
интегрируема по Риману на сегменте  , то по критерию Лебега мера Лебега точек розрыва
, то по критерию Лебега мера Лебега точек розрыва  на этом сегменте равняется 0. На сегменте
на этом сегменте равняется 0. На сегменте 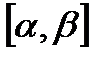 их не может быть больше, чем на
их не может быть больше, чем на  , поэтому мера Лебега точек разрыва
, поэтому мера Лебега точек разрыва  на
на 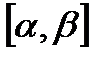 тоже равняется 0, а потому
тоже равняется 0, а потому  интегрируема по Риману на сегменте
интегрируема по Риману на сегменте 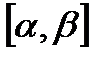 .
.
3. Пусть функция 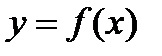 интегрируема по Риману на сегменте
интегрируема по Риману на сегменте  , тогда
, тогда 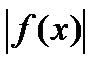 также интегрируема по Риману на сегменте
также интегрируема по Риману на сегменте  , к тому же
, к тому же
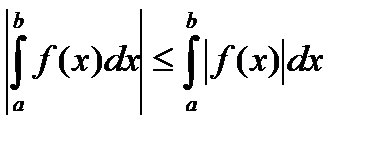 .
.
Доказательство. Поскольку  интегрируема по Риману на сегменте
интегрируема по Риману на сегменте  , то по критерию Лебега мера Лебега точек розрыва
, то по критерию Лебега мера Лебега точек розрыва  на этом сегменте равняется 0. Функция
на этом сегменте равняется 0. Функция 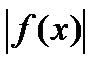 не может иметь разрывов больше, чем
не может иметь разрывов больше, чем  . Примеры построения графика функции
. Примеры построения графика функции 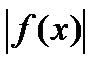 с использованием графика
с использованием графика  приведены на рис.1 (для получения графика
приведены на рис.1 (для получения графика 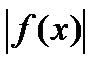 та часть графика
та часть графика  , которая находится в нижней координатной полуплоскости, отображается симметрично относительно оси ОХ) (черным цветом нарисован график данной функции
, которая находится в нижней координатной полуплоскости, отображается симметрично относительно оси ОХ) (черным цветом нарисован график данной функции  , красным - части графика
, красным - части графика 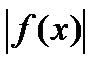 , которые изменяются относительно графика
, которые изменяются относительно графика  ).
).
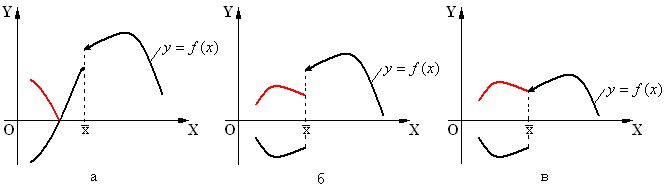
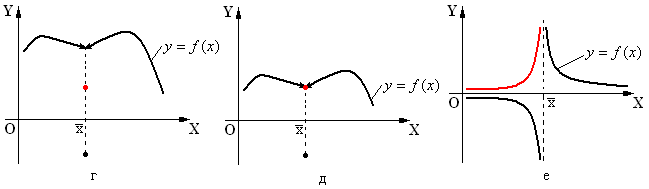
Рис.1.
Задание. Посмотрите внимательно, какие изменения произошли (или не произошли) в точках разрыва функций на рис.1.
Поскольку количество точек разрыва для функции 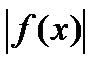 относительно
относительно  не возрастает, то мера Лебега множества точек разрыва
не возрастает, то мера Лебега множества точек разрыва 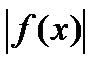 также будет равняться 0, а потому функция
также будет равняться 0, а потому функция 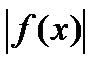 будет интегрируемой по Риману.
будет интегрируемой по Риману.
По свойствам модуля имеем: для 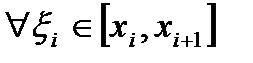
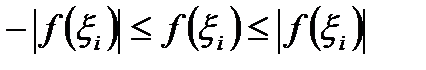 . (10)
. (10)
Умножим неравенство (10) на 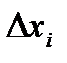 (поскольку
(поскольку 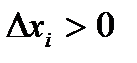 , знаки неравенства не изменятся) :
, знаки неравенства не изменятся) :
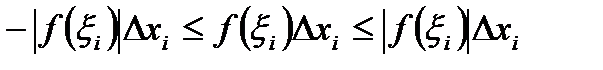 . (11)
. (11)
Неравенство (11) может быть получено для каждого частичного сегмента 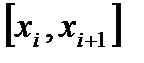 , где
, где 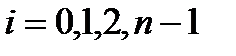 . Сложим эти неравенства. Получим:
. Сложим эти неравенства. Получим:
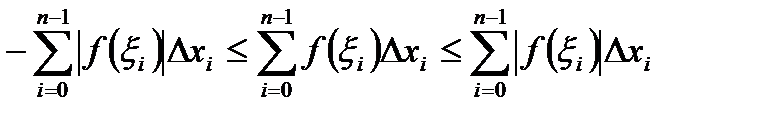 . (12)
. (12)
Средняя часть неравенства (12) - это интегральная сумма 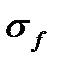 для функции
для функции  , левая и права части (12) - это
, левая и права части (12) - это 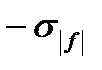 и
и 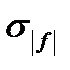 соответственно, где
соответственно, где 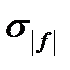 - интегральная сумма для
- интегральная сумма для 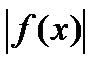 . Таким образом, неравенство (12) можно записать в виде:
. Таким образом, неравенство (12) можно записать в виде:
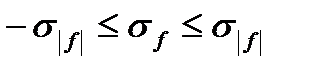 . (13)
. (13)
Переходя в неравенстве (13) к пределу, когда 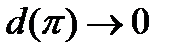 , учитывая, что функции
, учитывая, что функции  и
и 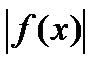 интегрируемы по Риману и определение интеграла Римана, получаем:
интегрируемы по Риману и определение интеграла Римана, получаем:
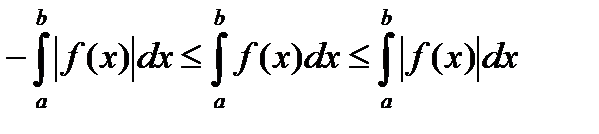 ,
,
откуда, пользуясь функцией модуля:
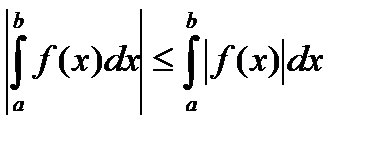 .
.
4. Пусть функция 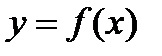 интегрируема по Риману на сегменте
интегрируема по Риману на сегменте  и
и 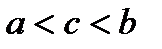 , тогда
, тогда
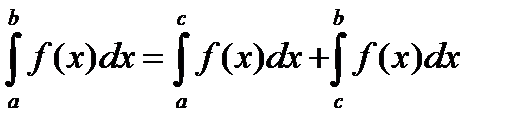 .
.
Определение 1. Пусть 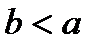 и функция
и функция 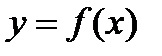 определена и интегрируема по Риману на сегменте
определена и интегрируема по Риману на сегменте 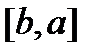 , тогда
, тогда
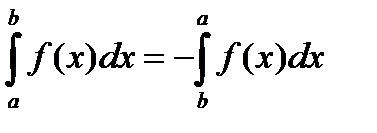 .
.
Определение 2. Для 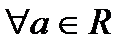
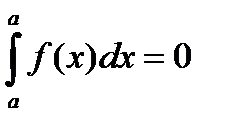 .
.
5. (Аддитивность интеграла Римана).
При любом взаимном расположении точек 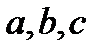 имеет место равенство:
имеет место равенство:
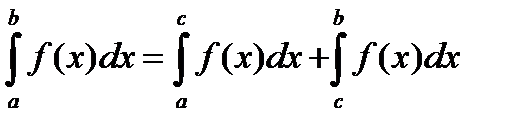 .
.
Доказательство. Рассмотрим какое-то конкретное взаимное расположение точек 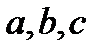 , например,
, например, 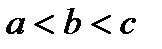 . Тогда по свойству 4, учитывая, что именно точка
. Тогда по свойству 4, учитывая, что именно точка 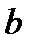 находится между
находится между 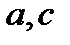 , имеем:
, имеем:
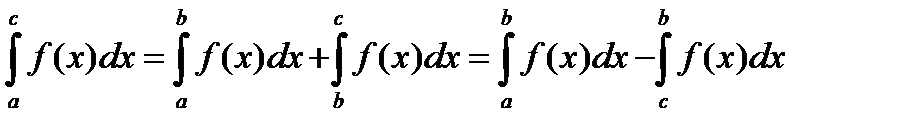 ,
,
т.е.
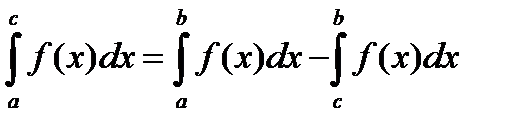 .
.
Перенося из правой части последнего равенства слагаемое 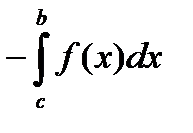 влево с противоположным знаком, получим:
влево с противоположным знаком, получим:
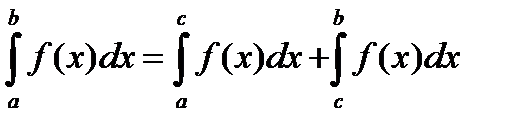 .
.
6. (Линейность интеграла).
Пусть функции 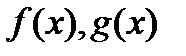 интегрируемы по Риману на сегменте
интегрируемы по Риману на сегменте  и пусть
и пусть 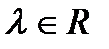 , тогда функции
, тогда функции 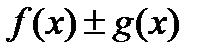 ,
, 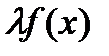 также являются интегрируемыми по Риману на
также являются интегрируемыми по Риману на  , и выполняются равенства:
, и выполняются равенства:
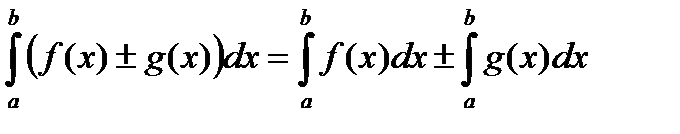 ,
,
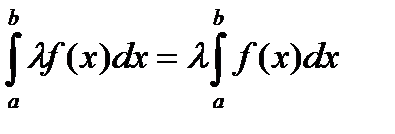 .
.
7. Пусть функции 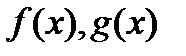 интегрируемы по Риману на сегменте
интегрируемы по Риману на сегменте  . Тогда
. Тогда 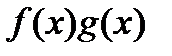 также интегрируемы по Риману на сегменте
также интегрируемы по Риману на сегменте  .
.
8. Пусть функции 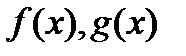 интегрируемы по Риману на сегменте
интегрируемы по Риману на сегменте  и для
и для 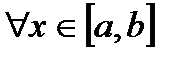
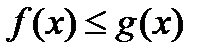 . Тогда
. Тогда
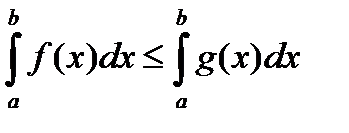 .
.
Задание. Показать, что если  определена и
определена и 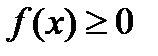 на сегменте
на сегменте  , то
, то
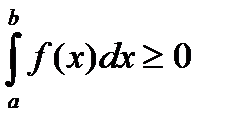 .
.
Завдание. Пусть  определена на сегменте
определена на сегменте  ,
, 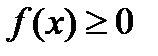 на сегменте
на сегменте  и
и 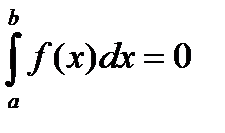 . Можно ли тогда утверждать, что
. Можно ли тогда утверждать, что 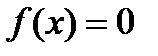 в каждой точке сегмента
в каждой точке сегмента  ? Почему?
? Почему?
9. (Первая теорема о среднем)
Пусть функция 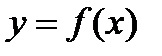 определена и интегрируема по Риману на сегменте
определена и интегрируема по Риману на сегменте  , а
, а 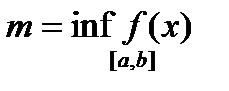 ,
, 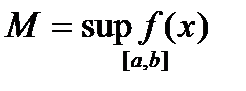 (поскольку по условию функция
(поскольку по условию функция 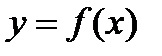 интегрируема по Риману на сегменте
интегрируема по Риману на сегменте  , то по необходимому условию интегрируемости, эта функция обязательно ограничена на сегменте
, то по необходимому условию интегрируемости, эта функция обязательно ограничена на сегменте  , а потому у нее существуют инфимум и супремум). Тогда
, а потому у нее существуют инфимум и супремум). Тогда
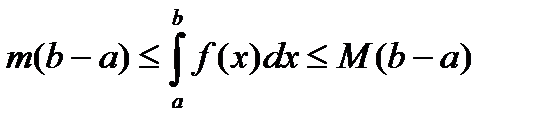 .
.
Доказательство. Пусть 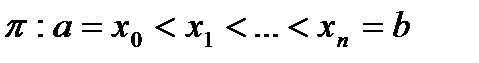 - произвольное разбиение сегмента
- произвольное разбиение сегмента  ,
, 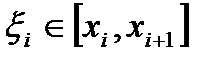 . Тогда
. Тогда
( 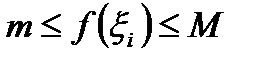 для
для 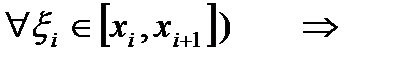
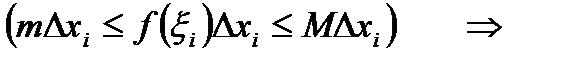
 .
.
Сумма 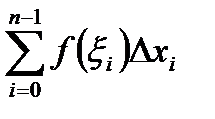 является интегральной суммой
является интегральной суммой  для функции
для функции  , а
, а 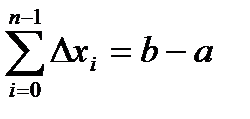 , тогда последняя формула может быть записана в виде:
, тогда последняя формула может быть записана в виде:
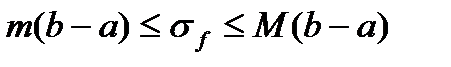 . (14)
. (14)
Если в формуле (14) перейти к пределу, когда 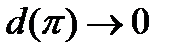 , то, учитывая, что
, то, учитывая, что 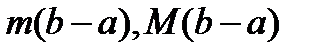 - это постоянные, а потому
- это постоянные, а потому
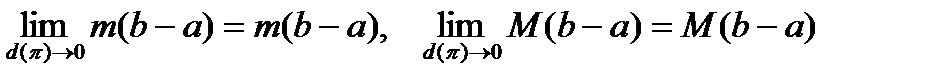 ,
,
а также, учитывая, что функция 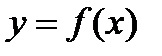 интегрируема по Риману на сегменте
интегрируема по Риману на сегменте  , получаем, что
, получаем, что
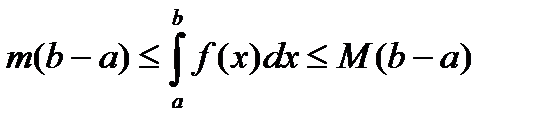 .
.
Следствие. Пусть функция 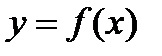 определена и интегрируема по Риману на сегменте
определена и интегрируема по Риману на сегменте  , а
, а 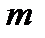 и
и 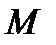 определены више. Тогда
определены више. Тогда 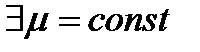
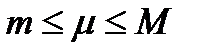 такое, что
такое, что
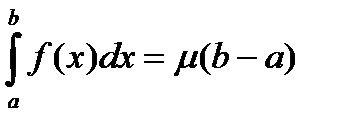 .
.
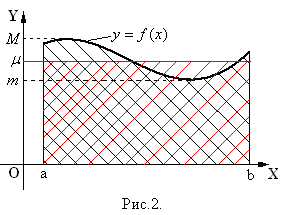 Геометрически это будет означать следующее: если функция
Геометрически это будет означать следующее: если функция 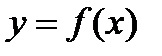 определена и интегрируема по Риману на сегменте
определена и интегрируема по Риману на сегменте  , то найдется такое число
, то найдется такое число 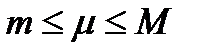 , что площадь криволинейной трапеции (на рис.1 эта площадь заштрихована черным цветом), которая ограничена графиком функции
, что площадь криволинейной трапеции (на рис.1 эта площадь заштрихована черным цветом), которая ограничена графиком функции 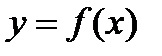 , осью ОХ и прямыми
, осью ОХ и прямыми 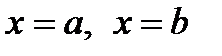 , будет численно равняться площади прямоугольника (на рис.1 эта площадь заштрихована красным цветом), стороны которого имеют длины
, будет численно равняться площади прямоугольника (на рис.1 эта площадь заштрихована красным цветом), стороны которого имеют длины 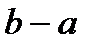 (это отрезок
(это отрезок  ) и
) и 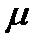 (див. рис.2).
(див. рис.2).
Пример. Оценить значение интеграла
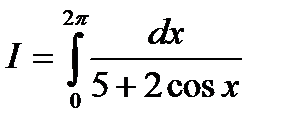 ,
,
не вычисляя его.
Для данного интеграла 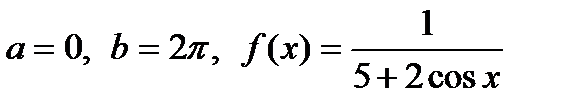 . Для его оценки воспользуемся первой теоремой о среднем. Для этого нам нужно найти инфимум и супремум функции
. Для его оценки воспользуемся первой теоремой о среднем. Для этого нам нужно найти инфимум и супремум функции 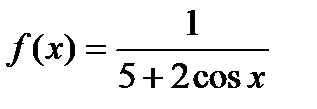 на сегменте
на сегменте  :
:
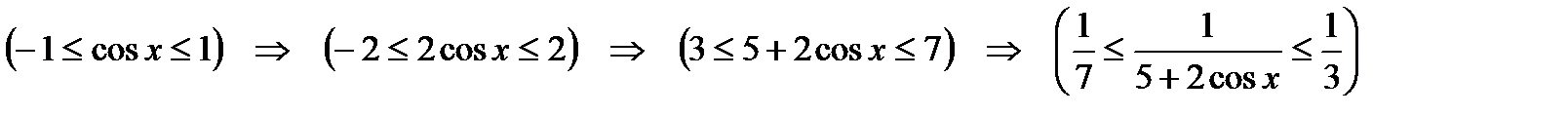 .
.
Таким образом, 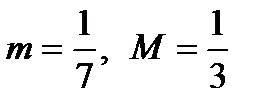 ,
, 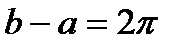 . Тогда
. Тогда
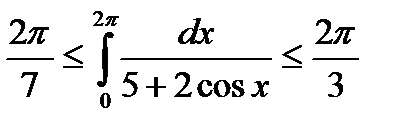 .
.
Задание. Не вычисляя непосредственно, оценить значение интеграла 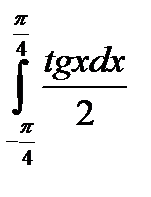 .
.
10. (Обобщенная теорема о среднем)
Пусть функции 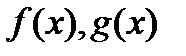 интегрируемы по Риману на сегменте
интегрируемы по Риману на сегменте  и выполняются условия:
и выполняются условия:
а) 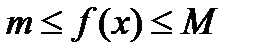 для
для 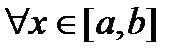 ;
;
б) 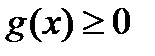 или
или 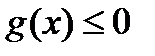 для
для 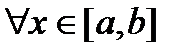 .
.
Тогда 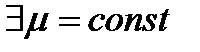
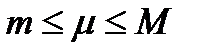 такая, что
такая, что
 . (15)
. (15)
Доказательство. Предположим сначала, что 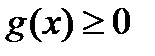 для
для 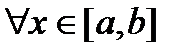 . По первому условию
. По первому условию
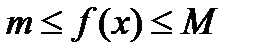 .
.
Учитывая, что 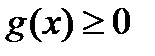 , умножим последнее неравенство на
, умножим последнее неравенство на 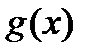 , оставивши знаки неравенства неизменными:
, оставивши знаки неравенства неизменными:
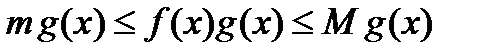 . (16)
. (16)
Поскольку 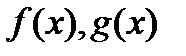 интегрируемы по Риману на сегменте
интегрируемы по Риману на сегменте  , то по свойству 7,
, то по свойству 7, 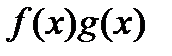 также интегрируема по Риману на сегменте
также интегрируема по Риману на сегменте  . Тогда, учитывая свойство 8, проинтегрируем неравенство (16) по Риману на
. Тогда, учитывая свойство 8, проинтегрируем неравенство (16) по Риману на  :
:
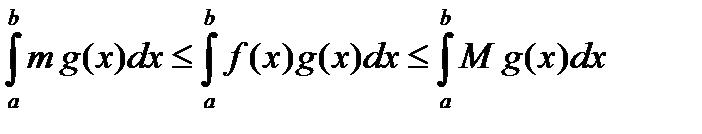 . (17)
. (17)
Учитывая свойство 6, вынесем постоянные множители за знак интеграла, тогда (17) будет иметь вид:
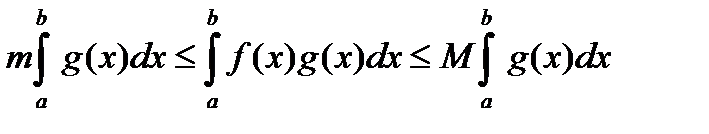 . (18)
. (18)
Поскольку по предположению 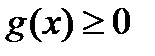 , то и
, то и 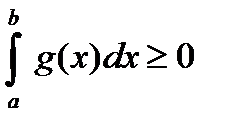 , то есть возможны два варианта:
, то есть возможны два варианта:
1. 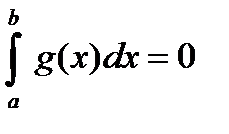 ; 2.
; 2. 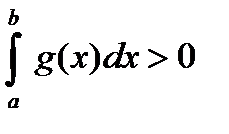 .
.
Рассмотрим первый вариант. Если 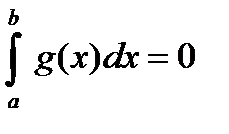 , то (18) будет иметь вид:
, то (18) будет иметь вид:
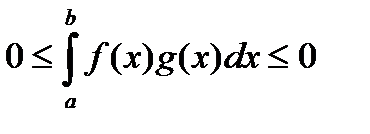 ,
,
а это возможно только тогда, когда  .Тогда
.Тогда
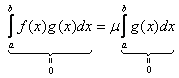
и как 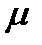 можно взять любую постоянную, то есть в этом случае теорема имеет место.
можно взять любую постоянную, то есть в этом случае теорема имеет место.
Рассмотрим второй вариант. Поскольку 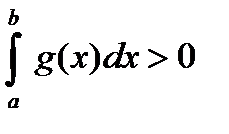 , то можно поделить почленно неравенство (18) на
, то можно поделить почленно неравенство (18) на 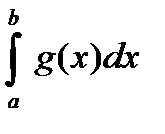 и при этом знаки неравенства останутся неизменными:
и при этом знаки неравенства останутся неизменными:
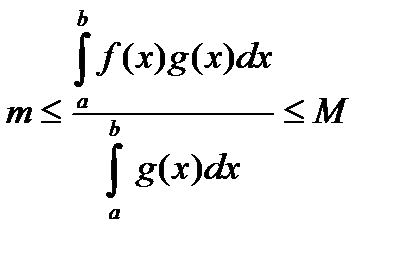 . (19)
. (19)
Если через 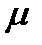 обозначить
обозначить
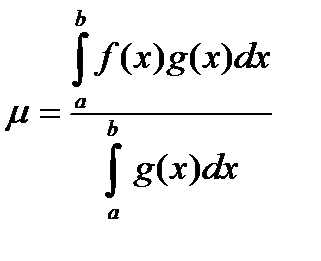 , (20)
, (20)
то из (19) 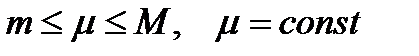 , а из (20)
, а из (20)
 ,
,
т.е. найденная постоянная 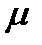 удовлетворяет всем требованиям.
удовлетворяет всем требованиям.
Пусть теперь 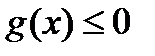 , тогда
, тогда 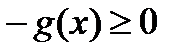 и для такой функция теорема уже доказана, то есть
и для такой функция теорема уже доказана, то есть 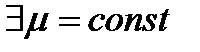
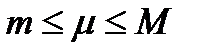 такое, что
такое, что
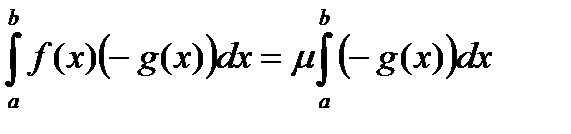 .
.
Пользуясь линейностью интеграла Римана, вынесем -1 (постоянный множитель) за знак интеграла:
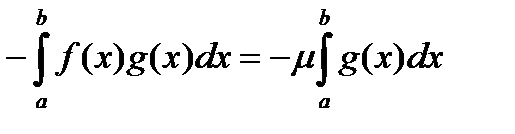 ,
,
Умножим обе части полученного равенства на -1:
 ,
,
то есть теорема доказана и для случая, когда 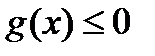 .
.
Дата добавления: 2015-08-21; просмотров: 1676;
