Достаточные условия интегрируемости функции по Риману

Теорема 2.Пусть функция непрерывна на сегменте , тогда она интегрируема по Риману на .

Доказательство. Поскольку непрерывна на сегменте , то по теореме Кантора она равномерно непрерывна на . Возьмем 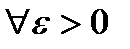, для него 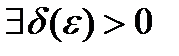такое, что для любого разбиения сегмента на частичные сегменты 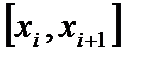такие, что 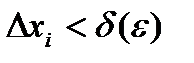, , 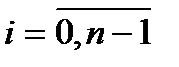будет иметь место неравенство: 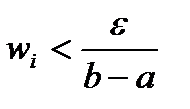. Тогда 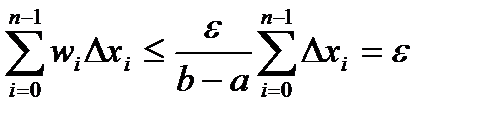, т.е.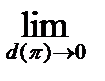 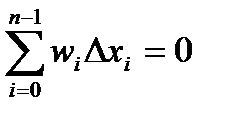, а - интегрируема по Риману.

Теорема 3. Пусть функция ограничена на сегменте и имеет на конечное количество точек разрыва. Тогда интегрируема по Риману на .

Визначення 1. Говорят, что множество точек 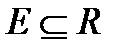имеет меру Жордана 0, если для 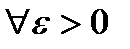существует конечная совокупность интервалов, которая покрывает множество 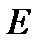, а сумма длин интервалов, которые входят в эту совокупность, не превышает .

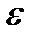Теорема 4. Если множество точек разрыва функции , которые принадлежат , имеют меру Жордана 0, то интегрируема по Риману на .

Пример. Рассмотрим функцию

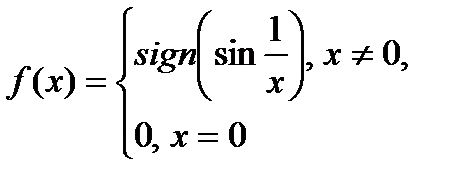
на сегменте 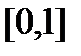. Найдем точки разрыва для функции на этом сегменте. Функция 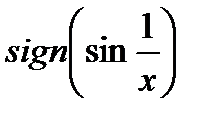является сложной и имеет точки разрыва там, где разрывы есть у внутренней или внешней функции. Поскольку при 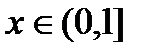функции 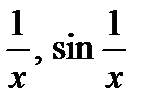являются непрерывными, то разрывы могут быть только благодаря разрывам внешней функции 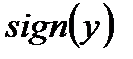, которые происходят при .

.

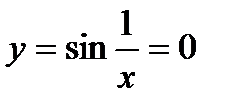Полученное множество точек разрыва 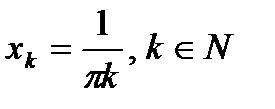имеет меру Жордана 0. Действительно, поскольку

,

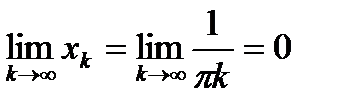то по определению предела последовательности это означает, что любая окрестность точки 0 ( 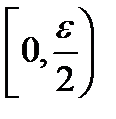)будет содержать все элементы последовательности, за исключением, возможно, конечного количества. Поэтому все множество точек разрыва можно покрыть конечным множеством интервалов суммарной длины меньше 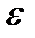. Таким образом, по теореме 4 функция интегрируема по Риману на .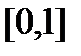

Теорема 5. Пусть функция определена и монотонна на сегменте . Тогда интегрируема по Риману на .

Доказательство. Пусть для определенносты монотонно возрастает на сегменте , а 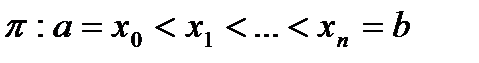- произвольное разбиение сегмента . Для монотонно возрастающей функции 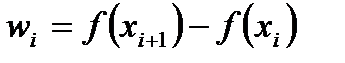. Возьмем произвольно 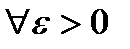. Пусть 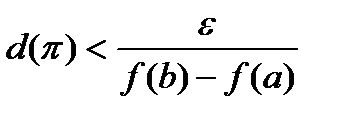. Тогда

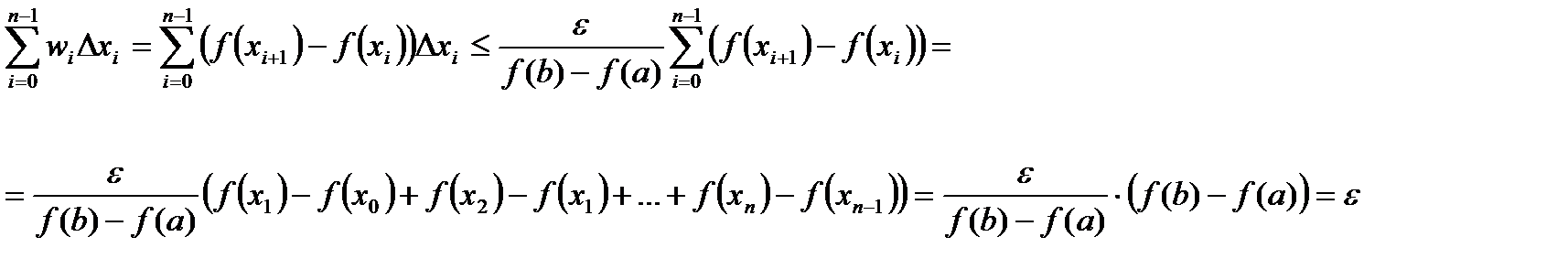
Это означает, что

,

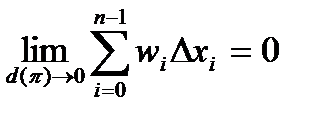т.е. интегрируема по Риману на по теореме 1.

Вывод. Пусть функция определена на сегменте и имеет место хотя бы одно из следующих условий:

1. непрерывна на ;

2. Множество точек разрыва функции имеет меру Жордана 0;

3. монотонна на ,

тогда интегрируема по Риману на .

Определение 2. Говорят, что множество точек 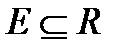имеет меру Лебега 0, если для 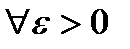существует конечная или счетная совокупность интервалов, которая покрывает множество 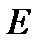, а сумма длин интервалов, которые входят в эту совокупность, не превышает .

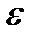Теорема 6 (Критерий Лебега). Для того, чтобы функция була интегрируема по Риману на необходимо и достаточно, чтобы множество ее точек разрыва на имело меру Лебега ноль.