Суммы Дарбу. Связь между интегральными сумами и сумами Дарбу
Нехай функция  определена и ограничена на
определена и ограничена на  , и пусть дано произвольное разбиение:
, и пусть дано произвольное разбиение: 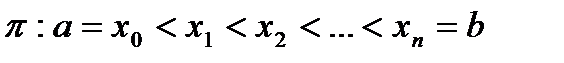 . Поскольку
. Поскольку  ограничена на
ограничена на  , то она ограничена на каждом частичном сегменте
, то она ограничена на каждом частичном сегменте 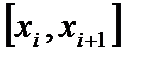 . Обозначим:
. Обозначим:
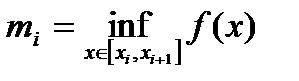 ,
, 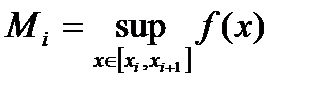 . (50)
. (50)
Построим суммы вида:
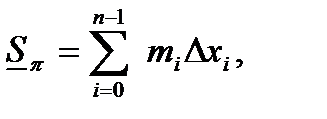
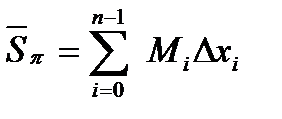 . (60)
. (60)
Определение 5. Суммы 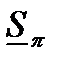 и
и 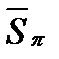 называются соответственно нижней и верхней суммами Дарбу для функции
называются соответственно нижней и верхней суммами Дарбу для функции  на
на  , которые отвечают заданному разбиению
, которые отвечают заданному разбиению 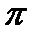 .
.
Замечание. Для любого разбиения 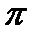 существует только одна нижняя и только одна верхняя суммы Дарбу (а интегральных сумм существует бесконечно много).
существует только одна нижняя и только одна верхняя суммы Дарбу (а интегральных сумм существует бесконечно много).
Пусть дано произвольное разбиение 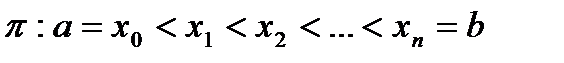 , а
, а 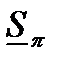 и
и 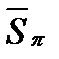 - нижняя и верхняя суммы Дарбу для функции
- нижняя и верхняя суммы Дарбу для функции  на
на  , которые отвечают заданному разбиению
, которые отвечают заданному разбиению 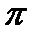 . Для
. Для 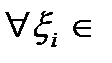
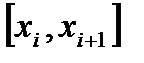 имеет место неравенство:
имеет место неравенство:
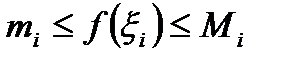 (70)
(70)
Умножим неравенство (70) на 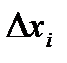 и возьмем сумму по всем
и возьмем сумму по всем 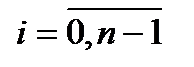 :
:
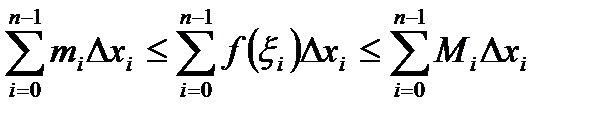 , (80)
, (80)
т.е. 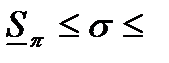
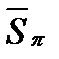 (90)
(90)
Всегда ли можно сказать, что суммы Дарбу являются интегральными сумами, то есть всегда ли на 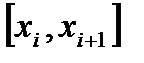 можно найти точку
можно найти точку 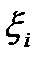 , что
, что  или
или  ? Ответ на вопрос - НЕТ. Действительно, если функция не является непрерывной, то она не всегда достигает на
? Ответ на вопрос - НЕТ. Действительно, если функция не является непрерывной, то она не всегда достигает на 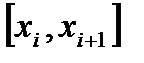 супремума или инфимума. Но в случае, когда
супремума или инфимума. Но в случае, когда  непрерывна на
непрерывна на  , а потому и на каждом частичном сегменте
, а потому и на каждом частичном сегменте 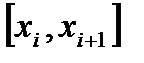 , по второй теореме Вейерштрасса она достигает на каждом
, по второй теореме Вейерштрасса она достигает на каждом 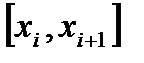 супремума и инфимума, а суммы Дарбу здесь одновременно будут интегральными сумами.
супремума и инфимума, а суммы Дарбу здесь одновременно будут интегральными сумами.
В общем случае 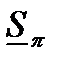 и
и 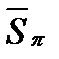 являются соответственно инфимумом и супремумом для множества всех интегральных сумм, построенных для данного разбиения
являются соответственно инфимумом и супремумом для множества всех интегральных сумм, построенных для данного разбиения 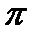 .
.
Дата добавления: 2015-08-21; просмотров: 1075;
