Построение интегральной суммы. Определение интеграла Римана

Лекция 15. Определенный интеграл Римана

План

Построение интегральной суммы. Определение интеграла Римана

Необходимое условие интегрированности функции по Риману

Суммы Дарбу. Связь между интегральными сумами и сумами Дарбу

Простейшие свойства сумм Дарбу. Крайние интегралы Дарбу

Построение интегральной суммы. Определение интеграла Римана

Пусть функция определена на . Пусть определено множество точек 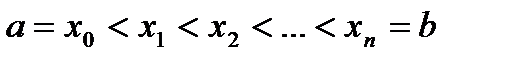. Каждый такой набор будем называть разбиением сегмента на частичные сегменты 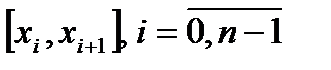иобозначать:

.

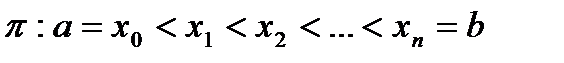Определение 1. Диаметром разбиения 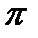будем называть самую большую из длин частичных сегментов :

.

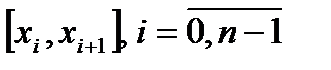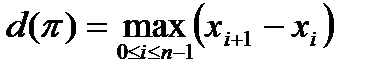Пусть 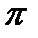- разбиение : 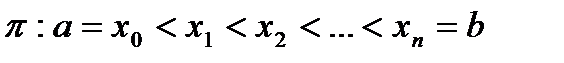. Выберем в каждом частичном сегменте 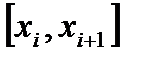произвольно точку 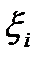, вычислим 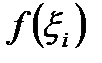и построим сумму:

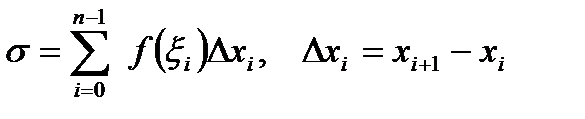(10)

Сумма (10) называется интегральной суммой для функции на , которая отвечает заданному разбиению и заданному выбору точок 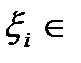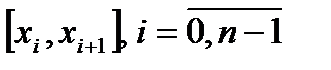. Понятно, что для функции на существует бесконечное множество интегральных сумм даже для заданного разбиения благодаря произвольности точек .

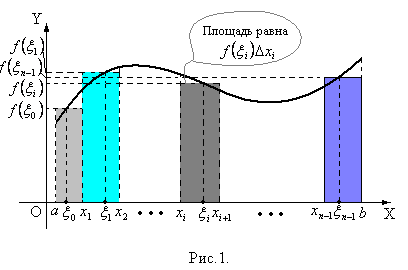
Геометрический смысл интегральной суммы.

Как видно из рис.1, 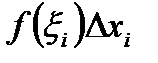- это площадь прямоугольника, длина одной стороны которого равняется 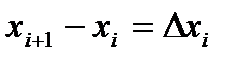, а высота – это 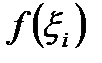. Тогда интегральная сумма (10) - это площадь ступенчатой фигуры, изображенной на рис.1.

Определение 2. Говорят, что число 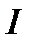является пределом интегральных сумм (10), когда 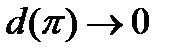, еслидля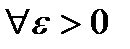 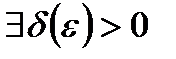такое, что 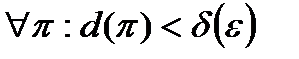будет выполняться неравенство:

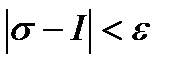(20)

для любого выбора точек 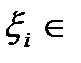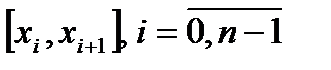(то есть предел не зависит ни от того, как именно сегмент разбивается на частичные сегменты, ни от того, как именно выбираются 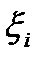. В этом случае будем писать, что

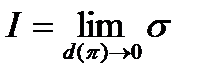. (30)

Существует еще одно определение предела интегральных сумм в терминах последовательностей:

Определение 3. Говорят, что число 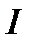является пределом интегральных сумм (10), когда 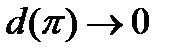, если для любой последовательности разбиений сегмента 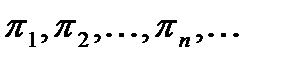, для которой 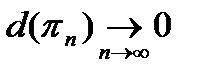, соответствующая последовательность интегральных сумм (10) стремится к 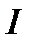: независимо от выбора точек .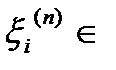

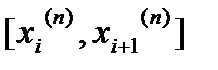Определение 4. Если предел (30) существует, то функцию называют интегрированной по Риману на , а число 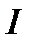называют ее интегралом Римана и обозначают:

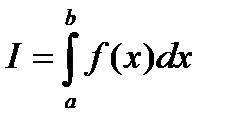. (40)

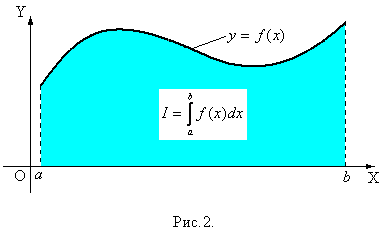Из определения 4 вытекает, что геометрический смысл интеграла Римана 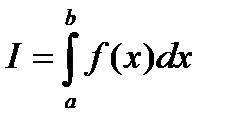– это площадь криволинейной трапеции, ограниченной графиком функции 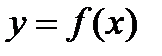, прямыми 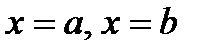, и осью ОХ (рис.2).