Простейшие свойства сумм Дарбу. Крайние интегралы Дарбу
Теорема 2. Пусть задано разбиение 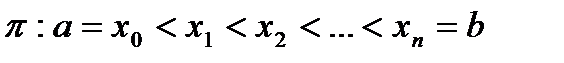 . Если к этим точкам разбиения добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя не возрастет.
. Если к этим точкам разбиения добавить новые точки, то нижняя сумма Дарбу не уменьшится, а верхняя не возрастет.
Доказательство. Докажем для случая, когда к разбиению 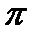 добавляется одна точка
добавляется одна точка 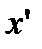 (поскольку тогда добавление любого количества точек можно будет провести по индукции). Получим разбиение
(поскольку тогда добавление любого количества точек можно будет провести по индукции). Получим разбиение  . Докажем, что
. Докажем, что 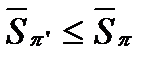 .
.
Пусть 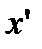 попадает в некоторый частичный сегмент
попадает в некоторый частичный сегмент 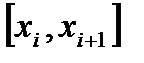 , при этом
, при этом
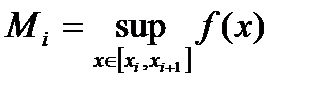 ,
, 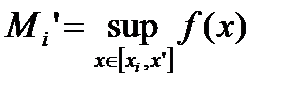 ,
, 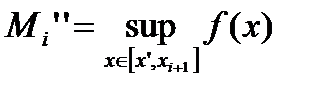 .
.
Верхние суммы Дарбу, которые отвечают разбиениям 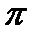 и
и 
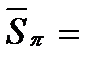
 (95)
(95)
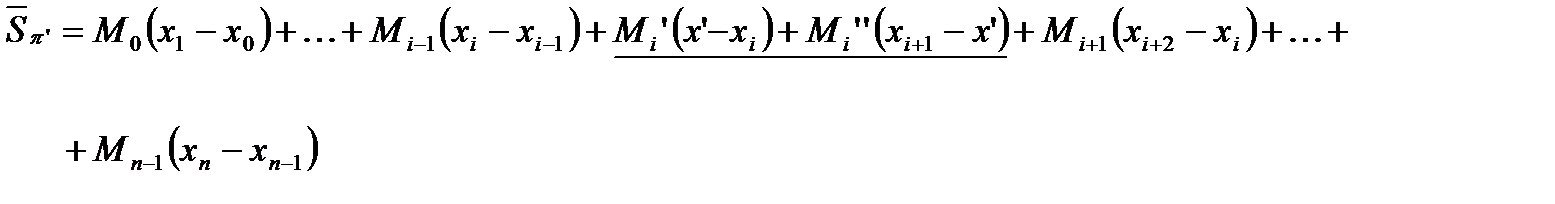 (96)
(96)
отличаются одна от другой лишь теми слагаемыми, которые подчеркнуты в формулах (95) и (96). Поскольку 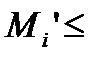
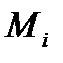 ,
, 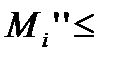
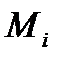 , то
, то
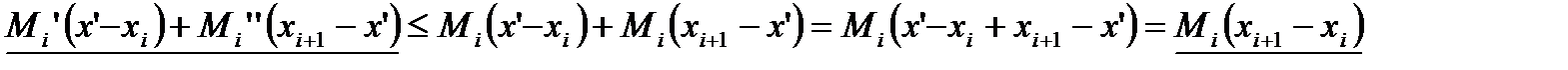 ,
,
откуда получаем, что 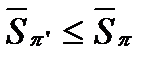 , что и нужно было доказать.
, что и нужно было доказать.
Теорема 3. Любая нижняя сумма Дарбу не превышает любой верхней суммы Дарбу, если они даже отвечают разным разбиениям.
Доказательство. Если 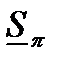 и
и 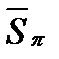 - нижняя и верхняя суммы Дарбу для функции
- нижняя и верхняя суммы Дарбу для функции  на
на  , которые отвечают одному разбиению
, которые отвечают одному разбиению 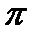 , то
, то
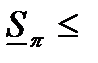
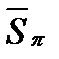 .
.
Пусть теперь есть два произвольных разбиения 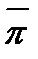 и
и 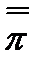 , и соответствующие им нижняя и верхняя суммы Дарбу:
, и соответствующие им нижняя и верхняя суммы Дарбу: 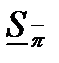 і
і 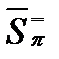 . Построим новое разбиение
. Построим новое разбиение 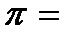
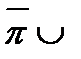
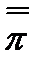 . Тогда:
. Тогда:
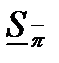
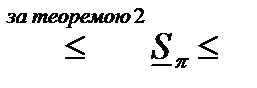
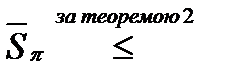
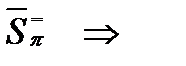
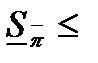
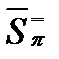 .
.
Пусть на  определена ограниченная функция
определена ограниченная функция  . Рассмотрим множество всевозможных разбиений этого сегмента и множества соответствующих этим разбиениям верхних и нижних сумм Дарбу. Пусть
. Рассмотрим множество всевозможных разбиений этого сегмента и множества соответствующих этим разбиениям верхних и нижних сумм Дарбу. Пусть 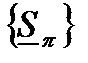 - множество нижних сумм Дарбу,
- множество нижних сумм Дарбу, 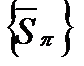 - множество верхних сумм Дарбу. Понятно, что множество
- множество верхних сумм Дарбу. Понятно, что множество 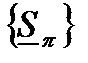 ограничено сверху любой верхней суммой Дарбу, а множество
ограничено сверху любой верхней суммой Дарбу, а множество 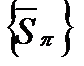 ограничено снизу любой нижней суммой Дарбу.
ограничено снизу любой нижней суммой Дарбу.
Определение 6. Нижним интегралом Дарбу называется:
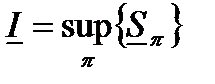 .
.
Определение 7. Верхним интегралом Дарбу называется:
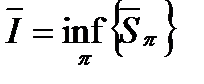 .
.
Определение 8. Нижний и верхний интегралы Дарбу называются крайними интегралами Дарбу. Если  ограничена, то они всегда существуют.
ограничена, то они всегда существуют.
Теорема 4. Пусть функция  ограничена на
ограничена на  , тогда
, тогда
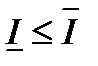 .
.
Теорема без доказательства.
Вопросы
1. Что называется разбиением сегмента? Сколько разных разбиений может иметь сегмент?
2. Что называется диаметром разбиения сегмента?
3. Как связаны между собой величина диаметра разбиения и количество частичных сегментов, образованных во время разбиения?
4. Что такое интегральная сумма для заданной функции на сегменте  ? Геометрический смысл интегральной суммы.
? Геометрический смысл интегральной суммы.
5. Сколько разных интегральных сумм существует для функции при заданном разбиении  сегмента
сегмента  ?
?
6. Что называется интегралом Римана для функции  на сегменте
на сегменте  ?
?
7. Когда функцию  называют интегрированной по Риману на
называют интегрированной по Риману на  ?
?
8. Необходимое условие интегрированности функции по Риману.
9. Определение нижней и верхней сумм Дарбу.
10. Сколько существует нижних и верхних сумм Дарбу при заданном разбиении сегмента?
11. Когда суммы Дарбу являются одновременно интегральными суммами?
12. Свойства сумм Дарбу.
13. Крайние интегралы Дарбу, их свойства.
Дата добавления: 2015-08-21; просмотров: 1194;
