Необходимое условие интегрированности функции по Риману

Теорема 1.Пусть функция определена и интегрирована по Риману на , тогда ограничена на .

Доказательство. Предположим, что функция определена и интегрирована по Риману на , но не ограничена на . Возьмем произвольное разбиение: 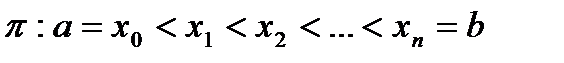. Поскольку не ограничена на , то она не ограничена хотя бы на одном частичном сегменте 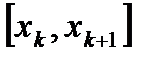. В каждом частичном сегменте 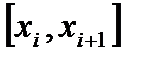, , 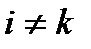(то есть за исключением 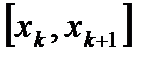) выберем промежуточные точки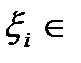 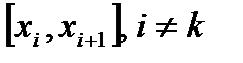. Построим сумму:

.

Тогда интегральную сумму можно записать в виде:

.

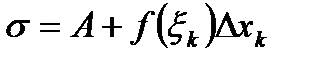Поскольку по предположению не ограничена на 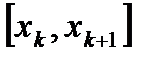, то сумму можно сделать путем выбора точки 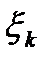как угодно большой, а это означает, что не имеет конечного предела, а потому функция не интегрирована по Риману на . Получили противоречие, поэтому предположение о неограниченности функции ложно.

Пример. Будет ли интегрированной по Риману на своей области определения функция:

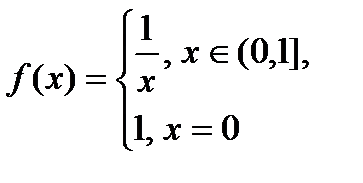
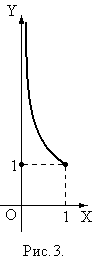
Область определения функции - сегмент 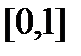. На этом сегменте является неограниченной (рис.3), а потому неинтегрированной по Риману.