Внутренняя энергия.

Согласно первому закону термодинамики, внутренняя энергия является однозначной функцией состояния системы. Внутренняя энергия системы зависит от внешних параметров и температуры и включает энергию движения всех микрочастиц системы и энергию их взаимодействия. В случае простейших систем с малым межмолекулярным взаимодействием (например, идеальный газ) изменение внутренней энергии сводится к изменению кинетической энергии молекул dU = C_VdT. Поэтому ∆Uдля идеального газа определяется только изменением температуры (закон Джоуля). В реальных системах, частицы которых взаимодействуют между собой (реальные газы, жидкости, кристаллы) внутренняя энергия включает также энергию межмолекулярных и внутримолекулярных взаимодействий.

Внутреннее давление, характеризующее зависимость внутренней энергии от объема при постоянной температуре, для любой системы (раздел 3.6) равно:

.

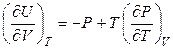Если система совершает только работу расширения, T и V – независимые параметры и внутренняя энергия зависит как от температуры, так и от объема 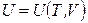, то в области непрерывности (в пределах существования одной фазы) выполняется соотношение

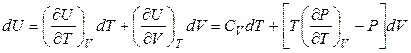. (4.27)

В точках фазовых переходов при T, P = const изменение (скачок) внутренней энергии вычисляют по экспериментальным величинам энтальпии перехода и изменения объема при переходе:

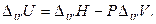(4.28)

Интегрируя уравнение (4.27) и принимая во внимание уравнение (4.28), можно получить выражение для расчета внутренней энергии вещества при заданных температуре и объеме:

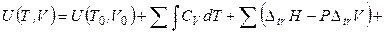
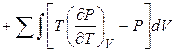. (4.29)

В выражении (4.29) суммирование относится к каждой фазе, а интегрирование – к интервалу существования данной фазы.

Далее, получим выражение, определяющее зависимость внутренней энергии от температуры при условии, что давление (а не объем) поддерживается постоянным. Пусть , тогда

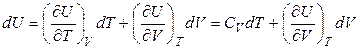. (4.30)

Разделим уравнение (4.30) на dT, а затем учтем условие постоянства давления:

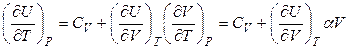, (4.31)

где 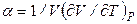– термодинамический коэффициент расширения.

Уравнение (4.31) имеет общее значение, так как дает возможность определить зависимость внутренней энергии любого вещества от температуры при постоянном давлении: необходимо только знать С_V, α и величину внутреннего давления. Экспериментальными методами можно измерить только изменение внутренней энергии, то есть определить внутреннюю энергию с точностью до постоянного слагаемого. При Т → 0 К внутренняя энергия конденсированных систем приближается к определенному постоянному значению U₀, которое может быть принято за начало отсчета внутренней энергии.

Для простых систем (выполняется только работа расширения) фундаментальное уравнение термодинамики записывается в виде:

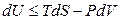; (4.32)

а для обратимых процессов:

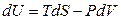. (4.33)

Следовательно, при V = const и S = const справедливо:

, .

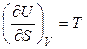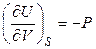Внутренняя энергия является характеристической функцией при независимых переменных S и V (S и V являются естественными переменными для внутренней энергии).

Выясним, как внутренняя энергия зависит от ее естественных переменных. Полагая V = const, получим:

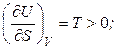
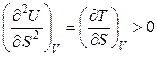. (4.34)

Температура является мерой возрастания внутренней энергии с увеличением энтропии при постоянном объеме. При этом функция U = f (S) является возрастающей, а кривая зависимости внутренней энергии от энтропии при постоянном объеме обращена выпуклостью вниз (рис. 4.1).

При постоянной энтропии системы (S = const) справедливо:

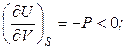
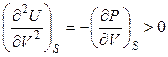. (4.35)

Функция U = f (V) при S = const является убывающей и кривая зависимости обращена выпуклостью вниз.

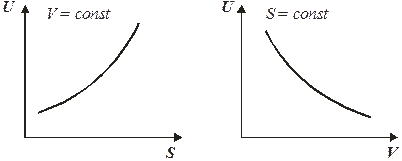
Рис. 4.1. Зависимость внутренней энергии от энтропии и объема.

Для систем, в которых, кроме работы расширения, может выполняться полезная работа, фундаментальное уравнение термодинамики запишется в виде:

. (4.36)

При S = const выполняется соотношение:

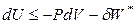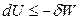, , (4.37)

где δW – полная работа.

Если процесс обратим, то выполняется максимальная работа δW_max, и уравнение (4.37) принимает вид:

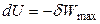или 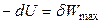. (4.38)

Следовательно, при условии постоянства энтропии в обратимых (изоэнтропийных) процессах убыль внутренней энергии равна количеству максимальной полной работы, произведенной системой.

Для обратимых процессов при S, V = const из (4.36) справедливо:

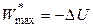, , (4.39)

то есть в изохорно-изоэнтропийных обратимых процессах за счет убыли внутренней энергии совершается максимальная полезная работа.