Характеристические функции.

Преобразование Лежандра позволило получить из фундаментального уравнения термодинамики (4.8) три новые функции, независимыми переменными которых являются P, S, V, T. Наиболее удобными с практической точки зрения являются функции A и G, так как их полные дифференциалы выражаются через основные параметры системы, то есть через те параметры, которые могут быть измерены (давление, температура, объем).

Характеристическими в термодинамике называются функции состояния, через производные которых наиболее просто и в явном виде могут быть выражены все термодинамические свойства системы. Особенности характеристических функций состоят в том, что свойством характеристичности они обладают при определенных независимых переменных, которые получили название естественных переменных (иногда их называют стандартными переменными). При другом выборе естественных независимых переменных функция теряет свойство характеристичности.

Покажем, что если энергия Гиббса выражена через Р и Т, т.е. естественными независимыми переменными функции G являются температура и давление, то она является характеристической функцией. Для обратимых процессов при условии, что выполняется только работа расширения, полный дифференциал энергии Гиббса равен

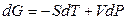, (4.20)

то есть 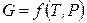; тогда при P = const или T = const, соответственно:

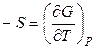, (4.21)

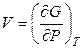. (4.22)

C другой стороны, справедливо:

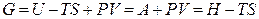. (4.23)

Следовательно,

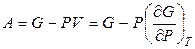, (4.24)

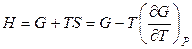, (4.25)

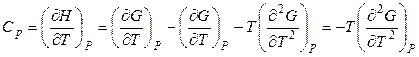. (4.26)

С учетом соотношения (4.21) выражение (4.26) можно записать как

.

Таким образом, энергия Гиббса, если независимыми переменными выбраны температура и давление, обладает свойством характеристической функции: все термодинамические свойства системы можно выразить в явном виде через функцию G и ее производные по естественным параметрам.

Функции U, H, S, A, G называются характеристическими. Необходимо подчеркнуть, что функции A и G образованы из функций состояния U, H, S и также являются функциями состояния, а их дифференциалы – полными дифференциалами.

Изменения характеристических функций U, H, A, G при определенных условиях, как будет показано, равны работе, поэтому их также называют термодинамическими потенциалами. При помощи термодинамических потенциалов выражают условия термодинамического равновесия и критерии его устойчивости. Вследствие важности характеристических функций для химической термодинамики, рассмотрим свойства каждой функции более подробно.