Уравнение Гиббса-Гельмгольца.

По определению энергии Гельмгольца и Гиббса равны

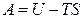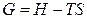, . (4.78)

Однако,

, ,

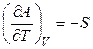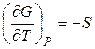поэтому соотношения (4.78) можно записать следующим образом:

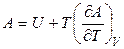, (4.79)

. (4.80)

Выражения (4.79) и (4.80) называются уравнениями Гиббса-Гель-мгольца и имеют практическое значение для изотермических процессов, протекающих с совершением полезной работы без видимого изменения объема.

Для обратимых процессов в закрытых системах, протекающих в изотермических условиях при постоянном давлении или постоянном объеме:

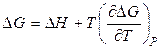, (4.81)

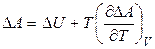. (4.82)

Эти соотношения являются термодинамическими тождествами, и если в них подставить значения

, , , ,

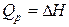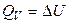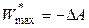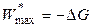то получим очень важные уравнения, связывающие величины полезной работы (суммs немеханических видов работ) с теплотами Q_P и Q_V:

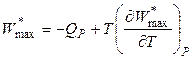, (4.83)

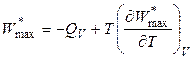. (4.84)

Уравнения (4.83) и (4.84) также называются уравнениями Гиббса-Гельмгольца или уравнениями максимальной работы. Они позволяют вычислить полезную работу по экспериментальным данным: тепловому эффекту реакции Q_P или Q_V и температурному коэффициенту работы.

Следует отметить, что в уравнениях (4.83) и (4.84) теплоты

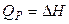и .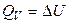

относятся не к тем процессам (обратимым), которым соответствует максимальная полезная работа. Эти величины относятся к процессам, протекающим между теми же начальными и конечными состояниями системы, но с совершением только работы расширения (W ^* = 0 для Q_p) или без совершения работы (W = 0 для Q_V) в неравновесных условиях (калориметрия). Теплоты же обратимого процесса, равные ТΔS, выражаются последними членами уравнений (4.83) и (4.84). Поэтому рассматриваемые уравнения можно записать и так:

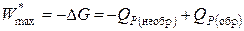, (4.85)

. (4.86)

Уравнения Гиббса-Гельмгольца (4.81) и (4.82) часто используют в виде, удобном для интегрирования. Объединим в левой части уравнения (4.81) ΔG и производную по температуре, разделим обе части уравнения на Т² и умножим на (–1), в результате получим

, ,

.

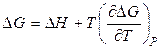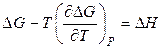Левая часть преобразованного уравнения равна производной по температуре от ΔG/T, поэтому

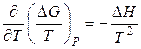. (4.87)

Разделив переменные и проинтегрировав уравнение (4.87), получим при постоянном давлении:

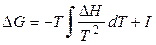или 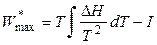, (4.88)

где I – константа интегрирования. Соотношение (4.88) используют для вычисления максимальной полезной работы процесса, необходимо только знать теплоту этого процесса и константу интегрирования.

Аналогично можно получить

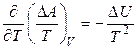. (4.89)