Соотношения Максвелла.
Если функции состояния U, H, A, G выразить через их естественные переменные, то они обладают свойством характеристичности и называются термодинамическими потенциалами. Их дифференциалы являются полными, и для простых систем при обратимом протекании процессов равны:
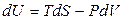 , (4.90)
, (4.90)
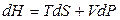 , (4.91)
, (4.91)
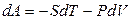 , (4.92)
, (4.92)
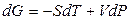 . (4.93)
. (4.93)
Используя независимость второй смешенной производной функции двух переменных от порядка дифференцирования, получим:
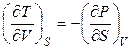 , (4.94)
, (4.94)
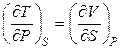 , (4.95)
, (4.95)
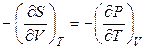 , (4.96)
, (4.96)
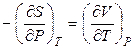 . (4.97)
. (4.97)
Соотношения (4.94) – (4.97) называютсяуравнениями Максвелла. Уравнения Максвелла могут быть записаны и в «перевернутом» виде:
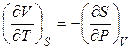 и т.д.
и т.д.
Все четыре уравнения Максвелла представляют собой, с одной стороны, производные энтропии или по давлению, или по объему, а с другой стороны, производные объема или давления по температуре. Уравнения Максвелла часто используются в математическом аппарате химической термодинамики.
Так, уравнения (4.96) и (4.97) используют для вычисления энтропии как функции Р и Т или V и Т. Например, для процесса изотермического повышения давления из (4.97) получаем
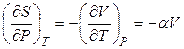 ,
,
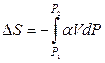 . (4.98)
. (4.98)
Если принять, что α и V конденсированной фазы не зависят от давления (жидкость или кристалл являются несжимаемым телом), то
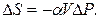 (4.99)
(4.99)
Уравнение (4.96) также может быть использовано в теории фазовых равновесий. Для гетерогенного равновесия давление является функцией одной переменной – температуры. Поэтому
 .
.
Значение рассматриваемой производной зависит только от температуры и при Т = const остается постоянной. Поэтому для фазового перехода соотношение (4.96) можно записать в следующем виде:
 ,
, 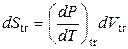 ,
,
а после интегрирования получаем
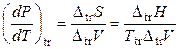 (4.100)
(4.100)
где ΔtrH – теплота фазового перехода, ΔtrV – изменение объема при переходе такого же количества вещества, к которому отнесено ΔtrH. Уравнение (4.100) и есть знаменитое уравнение Клапейрона-Клаузиуса.
Частные производные химической термодинамики чрезвычайно полезны при решении самых разнообразных задач. При этом следует помнить, что
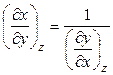 ,
, 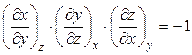 .
.
Например, требуется найти зависимость изобарной теплоемкости вещества от давления при постоянной температуре. С учетом преобразованного выражения (4.26) и соотношения (4.97)
 ,
, 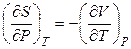 ,
,
получаем
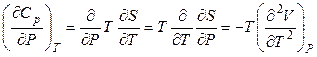 (4.101)
(4.101)
Таким образом, если наблюдается близкая к линейной зависимость объема от температуры, то изобарная теплоемкость не изменится. Для количественных расчетов необходимо иметь очень точное уравнение состояния данного вещества.
Другой пример: требуется определить, как изменится температура жидкости в результате ее адиабатического обратимого сжатия. Обратимый адиабатический процесс является изоэнтропийным, поэтому необходимо оценить производную 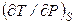 .
.
Если рассматривать 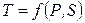 , то
, то
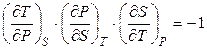 ,
,

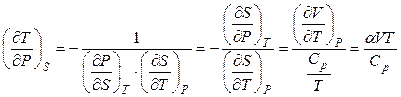 . (4.102)
. (4.102)
Дата добавления: 2015-08-20; просмотров: 1299;
