Энтальпия. Энтальпия (от греческого entalpo – нагреваю) – функция состояния, определяемая выражением

Энтальпия (от греческого entalpo – нагреваю) – функция состояния, определяемая выражением

.

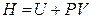Поскольку произведение PV равно потенциальной энергии расширения, то функцию Н можно назвать «энергией расширенной системы». Как экстенсивная величина энтальпия обладает свойством аддитивности, то есть энтальпия всей системы равна сумме энтальпий составляющих ее частей. Из первого закона термодинамики следует, что изменение энтальпии в изобарном процессе для простых систем равно теплоте этого процесса:

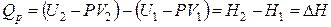. (4.40)

Изменение энтальпии равно количеству теплоты, которое сообщают системе или отводят от нее при P = const, поэтому ΔH характеризует тепловые эффекты фазовых переходов, химических реакций и других процессов. Этим объясняется широкое использование энтальпии в химии.

Для простой закрытой системы энтальпия будет однозначно определена, если заданы любые два параметра системы, определяющие ее состояние, например, Т и Р, т.е. Н = f (T, P). Тогда полный дифференциал энтальпии будет равен:

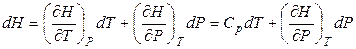. (4.41)

Найдем зависимость энтальпии от давления при постоянной температуре. Из выражений для первого и второго законов термодинамики

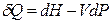и ,

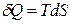следует, что

. (4.42)

Уравнение (4.42) можно рассматривать как объединенные первый и второй законы термодинамики для обратимых изменений состояния системы. Подстановка в уравнение (4.42) значения полного дифференциала dH согласно (4.41) приводит к выражению:

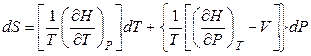. (4.43)

Используя свойства полного дифференциала dS (равенство перекрестных производных), можно записать:

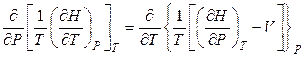, (4.44)

Дифференцируя выражение (4.44), получаем:

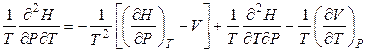, (4.45)

,

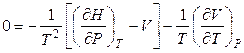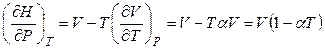, (4.46)

где α – изобарный термодинамический коэффициент расширения.

Следовательно, изменение энтальпии при изотермическом повышении давления можно вычислить по уравнению

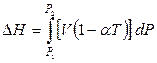. (4.47)

Проинтегрировав выражение (4.46) при условии постоянства температуры и определив исходное давление как Р₀, находим значение энтальпии при заданной температуре Т и давлении Р:

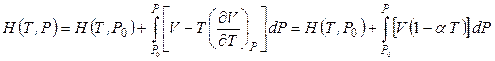. (4.48)

где Н(Т, Р₀) – энтальпия в начальном состоянии при Т и Р₀.

На основании первого и второго законов термодинамики можно вычислить не абсолютные значения характеристических функций, а их разности в каких-либо состояниях. Одно из состояний системы можно принять за стандартное (за начало отсчета) и вести расчет изменения функций от этого состояния.

Следовательно, величину изменения энтальпии с изменением температуры и давления можно получить, проинтегрировав уравнение (4.41) с учетом выражения (4.48):

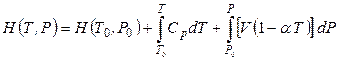, (4.49)

где Т₀, Р₀ – значение температуры и давления в стандартном состоянии.

Если в интервале температур от Т₀ до Т происходят фазовые превращения, то учитываются скачки энтальпии Δ_tr H при Т, Р = const:

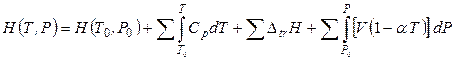, (4.50)

В выражении (4.50) суммирование относится к каждой фазе, а интегрирование – к интервалу существования фазы.

Полный диффренциал энтальпии для простых систем записывается в виде:

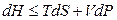. (4.51)

Для обратимых процессов выполняется следующее соотношение:

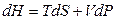, (4.52)

откуда

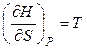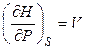, . (4.53)

Энтальпия является характеристической функцией, если выражена через ее естественные переменные S и P.

Функция Н = f (S) при Р = const является возрастающей, а кривая зависимости энтальпии от энтропии при постоянном давлении обращена выпуклостью вниз (рис.4.2), так как

, .

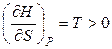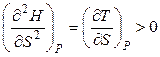Функция Н = f (P) при S = const тоже является возрастающей, но кривая зависимости энтальпии от давления при постоянной энтропии обращена выпуклостью вверх (рис.4.2), поскольку

, .

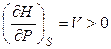Рис. 4.2. Зависимость энтальпии от энтропии и давления.

Для сложных систем (способных совершать полезную работу) справедливо следующее выражение:

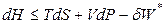. (4.54)

Поэтому, если обратимый процесс протекает при S, P = const, то

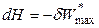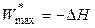, , (4.55)

то есть в изобарно-изоэнтропийных процессах максимальная полезная работа выполняется за счет убыли энтальпии.