Фундаментальные уравнения термодинамики. Преобразования Лежандра.
Глава 4. фундаментальные уравнения термодинамики. характеристические функции.
Фундаментальные уравнения термодинамики. Преобразования Лежандра.
Термодинамика как наука о наиболее общих свойствах макроскопических систем, находящихся в состоянии термодинамического равновесия, и о процессах перехода между этими состояниями построена просто – опытным путем установлены два ее основных закона, а применение к ним математического аппарата позволяет получить очень важные термодинамические соотношения.
Основой математического аппарата термодинамики является объединенное уравнение первого и второго законов термодинамики илифундаментальное уравнение Гиббса, которое для обратимых процессов записывается в виде
 , (4.1)
, (4.1)
где все параметры относятся к системе; PdV – механическая работа расширения системы; δW* – полезная работа системы (сумма немеханических видов работы, см. раздел 2.3)
Для простых систем в случае обратимых процессов фундаментальное уравнение записывается в виде
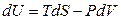 . (4.2)
. (4.2)
В математике независимыми переменными считаются те, которые стоят под знаком дифференциала. В фундаментальном уравнении (4.1) независимыми переменными являются S, V и все yk. Однако эти независимые параметры неудобны, так как энтропия непосредственно не измеряется, а объем легко определяется только для газов. Поэтому возникает задача перехода к новым независимым переменным.
Преобразование, меняющее ролями зависимые и независимые переменные, носит название преобразования Лежандра.
Рассмотрим функцию нескольких переменных:
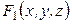 .
.
Полный дифференциал этой функции равен
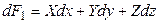 , (4.3)
, (4.3)
где
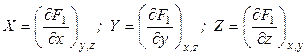 ,
,
причем X, Y, Z – функции x, y, z.
Введем новую функцию
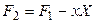 . (4.4)
. (4.4)
Полный дифференциал этой функции будет равен
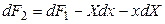 . (4.5)
. (4.5)
Подставив в равенство (4.5) значение dF1 из (4.3), получим:
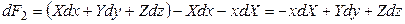 . (4.6)
. (4.6)
Cледовательно, в результате преобразования осуществлен переход от независимых переменных x, y, z к независимым переменным X, y, z, то есть переменная х стала зависимой, а Х – независимой. Кроме того, получили новую функцию F2. Таким образом, чтобы поменять зависимую переменную на независимую, следует воспользоваться соотношением
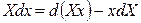 . (4.7)
. (4.7)
Впервые преобразование Лежандра к термодинамическим функциям применил Ф. Масье в 1869 году. Фундаментальное уравнение темодинамики для простых систем как для обратимых, так и для необратимых процессов запишется в виде:
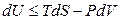 . (4.8)
. (4.8)
Знак неравенства используется для необратимых процессов, а знак равенства – для обратимых процессов. Применив к произведению PdV соотношение (4.7)
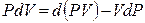 ,
,
получим:
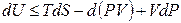 , (4.9)
, (4.9)
или
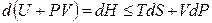 . (4.10)
. (4.10)
В результате перешли к независимым переменным S и Р и получили под знаком дифференциала в левой части (4.10) новую функцию
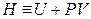 , (4.11)
, (4.11)
которая называется энтальпией.
Воспользовавшись подстановкой Лежандра для произведения TdS
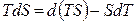 , (4.12)
, (4.12)
и подставив ее в фундаментальное уравнение (4.8), получим:
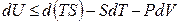 , (4.13)
, (4.13)
или
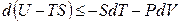 . (4.14)
. (4.14)
Стоящую под знаком полного дифференциала функцию U – TS обозначают по рекомендациям IUPAC символом Аи называютэнергией Гельмгольца(в некоторых учебниках энергию Гельмгольца до настоящего времени обозначают символом F):
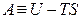 . (4.15)
. (4.15)
Итак, соотношение (4.14) записывается следующим образом:
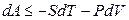 , (4.16)
, (4.16)
то есть в результате преобразований введена новая функция состояния при независимых переменных Т и V.
Преобразовав по Лежандру сразу оба произведения TdS и PdV в уравнении (4.8), получим:
 , (4.17)
, (4.17)
откуда
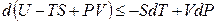 . (4.18)
. (4.18)
Функция U – TS + PV обозначается символом Gи называется энергией Гиббса. Следовательно, соотношение (4.18) запишется в виде:
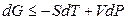 , (4.19)
, (4.19)
и энергия Гиббса является функцией независимых переменных Т и Р.
Дата добавления: 2015-08-20; просмотров: 3709;
