Энергия Гельмгольца.

Энергия Гельмгольца (изохорно-изотермический потенциал) является характеристической функцией, если независимыми переменными выбраны объем и температура. Полный дифференциал энергии Гельмгольца для простых систем записывается в виде:

, (4.56)

а в случае обратимых процессов как

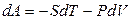. (4.57)

Полагая V = const, из уравнения (4.57) получаем

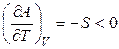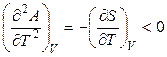, . (4.58)

Функция А = f (T) при V = const является убывающей, а кривая зависимости энергии Гельмгольца от температуры при постоянном объеме обращена выпуклостью вверх (рис. 4.3). Мерой убыли энергии Гельмгольца при повышении температуры вещества является энтропия.

Полагая Т = const, из уравнения (4.57) получаем

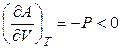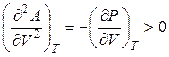, . (4.59)

Функция А = f (V) при T = const также является убывающей, но кривая зависимости энергии Гельмгольца от объема при постоянной температуре обращена выпуклостью вниз (рис. 4.3).

Рис.4.3. Зависимость энергии Гельмгольца от температуры и объема.

При протекании обратимых процессов в сложных системах, способных выполнять кроме работы расширения и другие виды работы (полезную работу), справедливо:

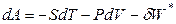. (4.60)

Если процесс изотермический (Т = const), то

,

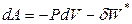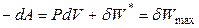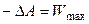, . (4.61)

Итак, в обратимом изотермическом процессе убыль энергии Гельмгольца равна максимальной (полной) работе, производимой системой. В этом заключается основной смысл введения новой функции А: через изменение функции состояния в изотермических условиях можно определить максимальную работу в обратимом процессе.

Если обратимый процесс протекает в изохорно-изотермических условиях, то

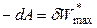, . (4.62)

В обратимом изохорно-изотермическом процессе убыль энергии Гельмгольца равна максимальной полезной работе.

Рассмотрим систему и окружающую среду, которые находятся в тепловом равновесии: Т_сист. = Т_ср.. Пусть в системе протекает процесс, в результате которого в окружающую среду переходит количество теплоты δQ_cр.. Тогда общее изменение энтропии dS_общ (ее называют изменением энтропии вселенной) равно:

.

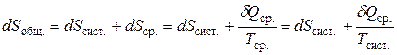Поскольку теплота уходит из системы, то δQ_cр. = –δQ_сист., поэтому

.

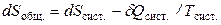Но dS_общ. положительно для любого самопроизвольного (необратимого) процесса и равно нулю при равновесии. Следовательно,

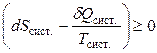. (4.63)

Значение неравенства (4.63) состоит в том, что оно выражает критерий самопроизвольного изменения только через свойства системы. Если система теряет теплоту при постоянном объеме, то

δQ_V = dU,

поэтому соотношение (4.63) принимает вид:

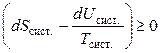или 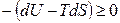. (4.64)

В последнем соотношении нижний индекс опущен, поскольку все величины относятся к системе. Следует понимать, что dS – это изменение энтропии системы, а ‑dU/T – изменение энтропии среды: суммарная энтропия стремится к максимуму.

Поскольку в конечном итоге рассматривается изохорно-изотерми-ческий процесс, то

.

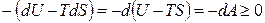Следовательно, при протекании процессов в изохорно-изотермических условиях должно выполняться неравенство

, (4.65)

где знак равенства относится к обратимым процессам, а знак неравенства – к необратимым.

Далее, для обратимого изотермического процесса

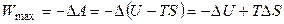. (4.66)

Если в обратимом процессе энтропия системы увеличивается, то максимальная работа больше, чем –ΔU, так как TΔS положительно. Система не изолирована и поэтому в нее может поступать теплота, служащая источником энергии для производства работы. Если же ΔS отрицательно, то теплота должна выделяться из системы, чтобы привести к общему увеличению энтропии (энтропии вселенной). Поэтому не все изменение внутренней энергии может перейти в работу и W_max < (–ΔU).