Энергия Гиббса.

Полный дифференциал энергии Гиббса для простых систем при протекании обратимых процессов равен

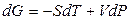.(4.67)

Энергия Гиббса является характеристической функцией, если независимыми переменными выбраны температура и давление. Функция состояния G наиболее чувствительна к изменению Т и Р, которые легче всего контролировать на практике, и отражает первый и второй законы термодинамики в наиболее удобном виде для применения в химии.

Рассмотрим, как энергия Гиббса зависит от температуры и давления (естественных переменных функции G). При постоянной температуре из уравнения (4.67) получаем

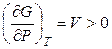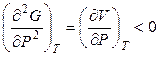, .(4.68)

Объем является мерой возрастания энергии Гиббса при изотермическом повышении давления. Функция G = f (P) при T = const является возрастающей, причем кривая зависимости обращена выпуклостью вверх (рис. 4.4).

При нагревании в изобарных условиях энергия Гиббса системы уменьшается, причем мерой ее убыли является энтропия системы:

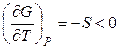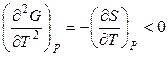, . (4.69)

Кривая зависимости энергии Гиббса от температуры при постоянном давлении обращена выпуклостью вверх (рис. 4.4).

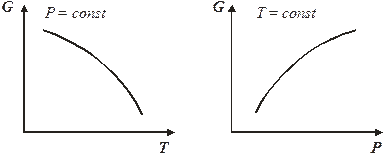
Рис. 4.4. Зависимость энергии Гиббса от температуры и давления.

Для сложной системы (совершающей полезную работу) при протекании обратимых процессов полный дифференциал энергии Гиббса записывается в следующем виде

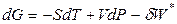. (4.70)

Если обратимый процесс протекает при постоянных температуре и давлении (в изобарно-изотермических условиях), то

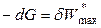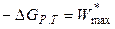, . (4.71)

Максимальная полезная работа в процессах при Р, Т = const равна убыли энергии Гиббса, поэтому ее также называют изобарно-изотермическим потенциалом.

Поскольку согласно (4.68)

,

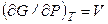то конечное изменение энергии Гиббса системы (вещества) при изотермическом повышении давления равно:

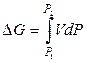. (4.72)

Если принять объем конденсированной фазы (жидкости или кристалла) не зависящим от давления, то

(4.73)

Получим общую формулу для расчета энергии Гиббса как функции температуры и давления: G = G(P, T). Согласно (4.68) и (4.26)

, .

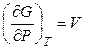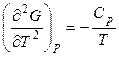Сначала найдем зависимость энергии Гиббса от давления при постоянной температуре Т, проинтегрировав уравнение (4.68):

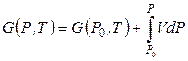. (4.74)

Путем интегрирования уравнения (4.26) найдем зависимость энергии Гиббса от температуры при постоянном давлении Р₀. Первое интегрирование (4.26) приводит к соотношению:

,

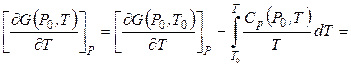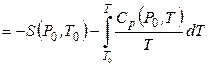, (4.75)

поскольку

,

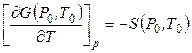где S(P₀,T₀) – значение энтропии при стандартных условиях.

После интегрирования уравнения (4.75) получаем:

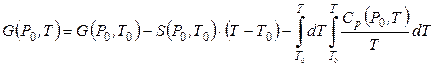. (4.76)

Окончательное выражение для значения энергии Гиббса G(P,T) получим, подставив соотношение (4.76) в уравнение (4.74):

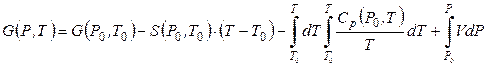. (4.77)