Важнейшие характеристические функции

Внутренняя энергия является первой термодинамической функцией, с которой мы познакомились. Кроме нее существуют и другие функции, приращение которых определяется приращением параметров системы. Иначе это свойство называют сопряжение по параметрам.

Так как внутренняя энергия сопряжена только по экстенсивным величинам и является единственной в своем роде функцией, то возникает вопрос: существует ли функция с сопряжением только по интенсивным величинам? Если такая функция существует, то она также должна быть единственной.

Обозначим возможную функцию с сопряжением только по интенсивным величинам Y и докажем, что такая функция должна иметь следующий вид:

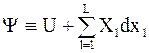. (5 - 7)

В выражении (5 - 7) символ тождества означает, что функция Y постулируется этим выражением (определяется этим выражением). Система обозначений, используемых в выражении (5 - 7) та же, что и в равенстве (5 - 4). В него включены все возможные пары параметров (их предполагаемое число равно L).

С учетом (5 - 4) найдем полное приращение функции Y.

;

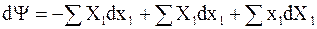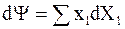. (5 - 8)

Выражение (5 - 8) показывает, что приращение функции определяется только приращением интенсивных величин.

Следовательно, функция Y является той единственной функцией, которая имеет сопряжение только по интенсивным величинам.

Между двумя крайними функциями (внутренней энергией и функцией Y) расположены функции, приращение которых зависит как от приращения экстенсивных величин, так и приращения интенсивных величин. Эти функции называются функциями со смешанным сопряжением.

Пусть F - общее обозначение функций со смешанным сопряжением. Покажем, что функции со смешанным сопряжением могут быть представлены общей формой

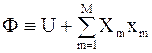. (5 - 9)

Выражение (5 - 9) по внешнему виду совпадает с выражением (5 - 7). Различие заключается в том, что в выражении (5 - 9) число слагаемых в сумме произведений экстенсивных и интенсивных величин меньше соответствующего числа слагаемых в выражении (5 - 7), т.е. M<L.

С учетом (5 - 4) приращение функций типа F можно представить следующим образом:

;

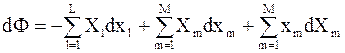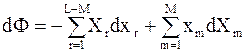. (5 - 10)

Выражение (5 - 10) показывает, что приращение функции F частично определяется приращением экстенсивных величин и частично приращением интенсивных величин.

Из функций со смешанным сопряжением наибольшее значение имеют:

энтальпия - функция, с которой мы уже неоднократно встречались,

H º U + PV (5 - 11)

энергия Гельмгольца

F º U - TS (5 - 12)

энергия Гиббса

G º U + PV - TS или G = Н - TS (5 - 13)

Запишем полное приращение этих функций вместе с приращением внутренней энергии:

dU = TdS - PdV - SX_idx_i; (5 - 14)

dH = dU + d(PV) = TdS - PdV - SX_idx_i+ PdV + VdP;

dH = TdS + VdP - SX_idx_i; (5 - 15)

dF = dU -d(TS) = TdS - PdV - SX_idx_i - TdS - SdT;

dF = -PdV - SdT - SX_idx_i; (5 - 16)

dG = dH -d(TS) = TdS + VdP - SXidxi - TdS - SdT;

dG = VdP - SdT - SX_idx_i. (5 - 17)

Сумма SX_idx_i представляет собой полезную работу квазистатического процесса. Как было отмечено раньше, работа квазистатического процесса является максимальной. В связи с этим выражения (5 - 14) - (5 - 17) можно записать в таком виде:

dU = TdS -PdV - dW`_max; (5 - 18)

dH = TdS + VdP -dW`_max; (5 - 19)

dF = -PdV - SdT - dW`_max; (5 - 20)

dG = VdP - SdT - dW`_max. (5 - 21)

В простых системах, в которых полезная работа отсутствует, полные приращения функций таковы:

dU = TdS - PdV; (5 - 22)

dH = TdS + VdP; (5 - 23)

dF = -PdV - SdT ; (5 - 24)

dG = VdP - SdT. (5 - 25)

Функции U, H, F и G замечательны тем, что их производные и приращения характеризуют состояние систем и происходящие в них процессы. В связи с этим для них используется общее название характеристические термодинамические функции.