Основные дифференциальные соотношения

Из равенств (5 - 22) - (5 - 25) следует

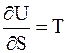; (5 - 26)

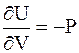; (5 - 27)

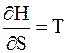; (5 - 28)

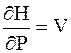; (5 - 29)

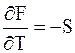; (5 - 30)

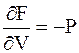; (5 - 31)

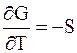; (5 - 32)

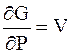. (5 - 33)

Частные производные характеристических функций широко используются при выводе термодинамических уравнений.

Равенства (5 - 26) - (5 - 33) могут быть использованы для установления зависимости между параметрами системы.

Для вывода этих уравнений воспользуемся основным свойством смешанных частных производных:

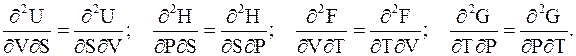В первом из вышеприведенных дифференциальных соотношений для внутренней энергии первая частная производная в левой части равенства согласно (5 - 27) равна - Р, а в правой части равенства в соответствии с (5 - 26) равна T. Далее в левой части проводится дифференцирование по S, а в правой части - по V. Тем же способом устанавливаются вторые частные производные для энтальпии, энергии Гельмгольца и энергии Гиббса.

Приведем окончательные результаты:

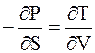; (5 - 34)

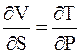; (5 - 35)

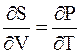; (5 - 36)

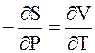. (5 - 37)

Дифференциальные уравнения (5 - 34) - (5 - 37), устанавливающие зависимость между параметрами системы, называются уравнениями Максвелла.