Метод циклов в термодинамике. Уравнение Клапейрона - Клаузиуса

Метод циклов, или метод круговых процессов, оказался первым методом, с помощью которого на основании первого и второго начал термодинамики были установлены важнейшие количественные соотношения для различных явлений.

Сущность этого метода заключается в подборе подходящего квазистатического цикла, по характеристикам которого удается получить зависимость между термодинамическими величинами.

Наиболее часто в методе круговых процессов используется квазистатический цикл Карно, для которого известен термодинамический КПД.

Общих правил применения метода циклов не существует. Поэтому подбор подходящего цикла для решения какой-либо конкретной задачи является своего рода искусством.

Покажем, как применяется метод циклов на примере вывода уравнения Клапейрона - Клаузиуса, устанавливающего зависимость между параметрами системы и теплотой (изменением энтальпии) фазового перехода.

Мысленно осуществим с 1 моль вещества цикл, состоящий из следующих стадий:

* фазовый переход (испарение, возгонка, плавление) при давлении Р от молярного объема исходной фазы V₁ до молярного объема конечной фазы V₂ (пусть, например V₁ - объем жидкости, а V₂ - объем пара; или V₁ - объем твердого вещества, а V₂ - объем жидкости и т.д.);

* адиабатическое снижение давления на dP (в связи со столь незначительным изменением давления объем конечной фазы практически не изменится);

* обратный переход конечной фазы в исходную (конденсация, кристаллизация) с изменением объема системы от V₂ до V₁;

* адиабатическое сжатие системы на dP (конденсированные системы можно считать несжимаемыми, и объем системы на этой стадии не изменяется).

Контуры этого цикла в координатах (давление, объем) представляют собой узкую полоску с шириной dP и длиной (V₂-V₁) . Площадь этой полоски равна работе цикла

dW^qs=(V₂-V₁)dP.

В этом цикле теплота к системе подводится только на первой стадии. Она представляет собой изменение энтальпии при фазовом переходе DH_p.t..

Термодинамический КПД рассматриваемого цикла равен

.

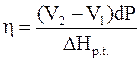Данный цикл является циклом Карно (первая и третья стадии осуществляются при постоянной температуре). Если температура фазового перехода равна Т, а изменение температуры при переходе от одной изотермы к другой равно dT, то этот же КПД должен быть равен

.

Так как левая часть обоих равенств является одной и той же величиной, то, приравнивая их правые части, получим

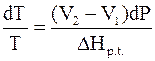
или

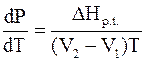. (4 - 16)

Уравнение (4 - 16) называется уравнением Клапейрона ‑ Клаузиуса.

В процессе испарения жидкости объемом жидкости по сравнению с объемом пара можно пренебречь (для сравнения: при нормальной температуре кипения 373 К молярный объем водяного пара в 930 раз превышает объем жидкой воды). Если же предположить, что пар приближается по свойствам к идеальному газу, то можно воспользоваться следующим приближением:

.

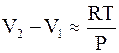С учетом этого приближения уравнение Клапейрона - Клаузиуса для процессов испарения и возгонки приобретает следующую форму:

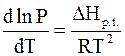. (4 - 17)

Приняв теплоту испарения постоянной, интегрированием уравнения (4 - 17) можно найти зависимость давления насыщенного пара от температуры. Она обычно выражается следующим образом:

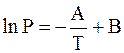, (4 - 18)

где А и В - константы, зависящие от природы вещества.

В настоящее время метод циклов употребляется редко. Его вытеснил более универсальный метод характеристических термодинамических функций, ранее называвшийся методом термодинамических потенциалов.