Изменение энтропии при протекании реальных процессов

По теплоте реальных процессов нельзя рассчитать изменение энтропии.

В связи с этим реальный процесс заменяется квазистатическим процессом, условно проводимым от общего для обоих процессов исходного состояния системы до общего для них конечного состояния.

Поясним изложенное примерами.

Истечение идеального газа в пустоту

Пусть в изолированной системе газ занимает первоначальный объем V₁. Затем он истекает в вакуум, и его объем увеличивается до V₂.

Поскольку газ изолирован от внешней среды, он не может получить теплоту извне. Истечение газа в пустоту не сопровождается работой. Следовательно, внутренняя энергия газа не изменится. В соответствии с законом Гей-Люссака - Джоуля при постоянной внутренней энергии температура также остается постоянной.

Итак, в исходном состоянии с объемом V₁ и конечном состоянии с объемом V₂ газ имеет одну и ту же температуру. Переход из одного из указанных состояний в другое может быть осуществлен изотермическим расширением газа в квазистатических условиях. В предыдущем параграфе было показано, что в этом случае можно воспользоваться формулой (4 - 13).

Так как конечный объем V₂ больше исходного объема V₁ и отношение V₂/V₁ больше 1, то

.

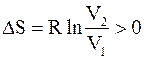Полученный результат означает, что изотермическое самопроизвольное расширение газа приводит к возрастанию его энтропии.

Самопроизвольное выравнивание температур

Пример 1.

Рассмотрим систему, состоящую из двух кусков металла, имеющих разные температуры Т₁ и Т₂. Для простоты расчетов положим, что теплоемкость обоих кусков C_V одинакова и не зависит от температуры, а количество вещества в каждом куске равно 1.

При контакте обоих кусков происходит выравнивание температур и устанавливается общая для них температура Т_е, равная средней арифметической исходных температур:

.

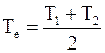Изменение энтропии каждого куска металла выразится следующим образом:

; .

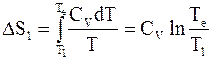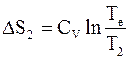Общее изменение энтропии находим как сумму изменений для каждого куска металла (используется свойство аддитивности энтропии)

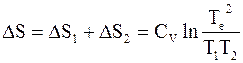. (4 - 15)

Числитель подлогарифмического выражения, как уже было показано, представляет собой квадрат средней арифметической величины от Т₁ и Т₂, а знаменатель - квадрат их средней геометрической. Так как средняя арифметическая величина больше средней геометрической, то

DS>0.

Пример 2.

Рассчитаем изменение энтропии при добавлении к 3,6 г воды, взятой при 298 К, 27 г льда, находящегося при 273 К.

Справочные данные: теплоемкость воды C_p равна 75,3 Дж/моль×К (принимается постоянной), изменение энтальпии при плавлении льда равно 6,0 кДж/моль.

Изменение энтальпии (теплота при постоянном давлении) воды при охлаждении от исходной температуры Т₁=298 К до температуры плавления льда Т₂=273 К рассчитывается по формуле

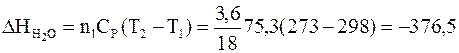Дж.

Рассчитаем количество льда, которое расплавится при поглощении теплоты, выделяемой водой:

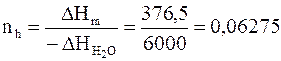моль.

Это количество меньше количества льда, имеющегося в системе, т.е. лед расплавится частично.

Изменение энтропии при плавлении льда в соответствии с формулой (4 - 14) составит

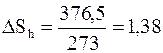Дж/ К.

Изменение энтропии воды рассчитаем по формуле (4 ‑ 12)

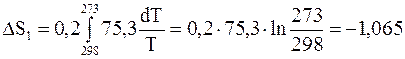Дж/ К.

Общее изменение энтропии находим, используя свойство аддитивности,

DS=DS_h +DS_l=1,38+(-1,065)=0,315 Дж/ К; DS>0.

Из рассмотренных примеров можно сделать вывод: при самопроизвольном выравнивании температур в системе ее энтропия возрастает.