Формулы Клаузиуса. Энтропия
Из теоремы Клаузиуса о сопряженных циклах следует, что для цикла Карно с любой системой применимо равенство
,
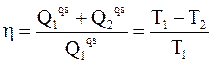в котором Q1qs - теплота, получаемая системой от теплового источника с температурой Т1, а Q2qs - теплота, поступающая к тепловому стоку с температурой Т2.
Таким образом, для цикла Карно с любым рабочим телом выполняется условие равенства нулю суммы приведенных теплот:
.
Для бесконечно малого расстояния между адиабатами равенство принимает следующую форму:
.
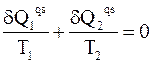Обратимся к проводимому квазистатически произвольному циклу.
Обозначим точки касания адиабат с контуром произвольного цикла (1) и (2), причем (1) - левая точка касания, а (2) - правая точка касания.
Заменив произвольный цикл бесконечной суммой пар бесконечно малых изотерм, для перехода от точки (1) к точке (2) можно записать:
.
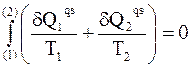Переход от точки (1) к точке (2) по парам изотерм означает смещение слева направо по верхним изотермам и одновременное смещение справа налево по нижним изотермам. В целом это составляет перемещение по замкнутому контуру. По этой причине предыдущее равенство можно заменить следующим:
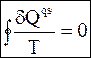. (4 - 1)
Уравнение (4 - 1) означает, что подынтегральное выражение представляет собой приращение функции состояния. Отметим, что приращение функции состояния не зависит от процесса. Введем для новой функции обозначение S. Следовательно,
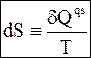. (4 - 2)
Введенная на основе второго начала термодинамики Р.Клаузиусом функция S называется энтропией.
Энтропия обладает основными свойствами функции состояния:
* приращение функции не зависит от процесса, а определяется только начальным и конечным состоянием системы,
* функция аддитивна, т.е. ее величина (или приращение) представляет собой сумму энтропий (или приращений энтропии) для отдельных частей системы .
Размерность энтропии -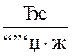 
.
Конечное приращение энтропии находится интегрированием
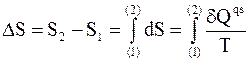. (4 - 3)
В формулах (4 - 1) - (4 - 3) используется теплота квазистатического процесса. Для нестатических (реальных ) процессов, как ранее было показано, выполняется условие
dWqs> dWr ,
из которого следует
dU+dWqs>dU+dWr,
так как приращение внутренней энергии, являющейся функцией состояния, не зависит от процесса. Поэтому
dQqs >dQr.
Следовательно,
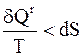; (4 - 4)
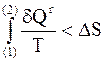; (4 - 5)
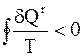. (4 - 6)
Формулы (4 - 1) - (4 - 6) называются формулами Клаузиуса.
Дата добавления: 2015-07-24; просмотров: 1190;