Второй закон (начало) термодинамики. Энтропия
Согласно первому закону термодинамики, могут протекать только такие процессы, при которых полная энергия системы остается неизменной. Например, превращение тепловой энергии целиком в механическую не связано с нарушением первого закона; тем не менее оно не возможно. Второй закон термодинамики еще больше ограничивает возможные процессы превращения.
Теплоту можно превратить в работу только при условии, что часть этой теплоты одновременно перейдет от горячего тела к холодному (принцип действия тепловых двигателей).
Устройство, которое вопреки этому закону получало бы тепловую энергию от нагревателя и производило равное количество механической энергии, называется вечным двигателем второго рода. (Пример: камень, который охлаждаясь поднимался бы вверх!)
Чтобы теплота могла перейти от холодного тела к горячему, необходимо затратить механическую работу (принцип действия холодильных машин). Отсюда следует, что в замкнутой системе в отсутствие каких-либо процессов не может сама по себе возникнуть и разность температур, т.е. теплота не может самопроизвольно перейти от более холодных частей системы к более горячим.
Все термодинамические процессы, протекающие в замкнутой системе, можно подразделить на обратимые и необратимые.
Термодинамический процесс обратим, если, протекая в обратном направлении, он возвращает систему в исходное состояние без затрат энергии.
В противном случае термодинамические процессы называются необратимыми. Они протекают самопроизвольно только в одном направлении.
Примеры обратимых процессов: движение планет, незатухающие колебания маятника, упругий удар, цикл Карно.
Примеры необратимых процессов: затухающие колебания маятника, неупругий удар, процессы с трением, диффузия, теплопередача, теплообмен.
Большинство процессов в технике представляют собой необратимые процессы или по крайней мере содержат этапы, являющиеся необратимыми процессами.
Из уравнений (9.32) и (9.35) для цикла Карно (обратимого) следует
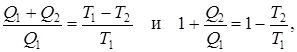
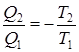 и наконец,
и наконец, 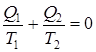 (9.36)
(9.36)
Это уравнение означает, что количество теплоты, полученное или отданное телом при обратимом процессе, пропорционально температуре.
Отношение Q/T называется приведенным количеством теплоты.
Сумма приведенных количеств теплоты при любом обратимом процессе равна нулю:
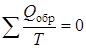 , (9.37)
, (9.37)
или в дифференциальной форме
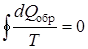 . (9.38)
. (9.38)
Знак 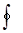 означает, что интеграл берется по замкнутому контуру (круговой процесс).
означает, что интеграл берется по замкнутому контуру (круговой процесс).
В каждом цикле обратимого процесса все термодинамические параметры принимают исходные значения, т.е. их изменение равно нулю, можно определить термодинамический параметр состояния — энтропию S как функцию, дифференциал которой равен
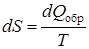 . (9.39)
. (9.39)
Единица СИ энтропии 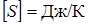 .
.
Поскольку в уравнения обычно входит не сама энтропия, а ее изменение, за нулевое значение энтропии в технике обычно произвольно принимают ее значение, соответствующее температуре 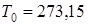
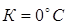 .
.
Воспользовавшись уравнением (9.39), получим следующее выражение для изменения энтропии при переходе из состояния 1 в состояние 2:
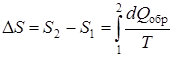 . (9.40)
. (9.40)
При обратимом процессе изменение энтропии 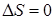 .
.
При необратимом процессе изменение энтропии 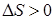 .
.
Все процессы в природе протекают в направлении увеличения энтропии.
Использование понятия энтропии позволяет очень просто сформулировать второй закон термодинамики:
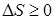 . (9.41)
. (9.41)
Энтропия замкнутой системы не может уменьшаться!
Неравенство (9.41) называется неравенством Клаузиуса.
Дата добавления: 2015-08-08; просмотров: 872;
