Внутренняя динамика
Понятие внутренней динамики введем с помощью следующего примера. Рассмотрим нелинейный объект управления
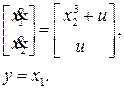 (21)
(21)
Цель управления, чтобы выход y(t) следил за yж(t). Дифференцируя y(t), получаем
 (22)
(22)
Отсюда управление
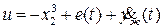 (23)
(23)
приводит к уравнению для ошибки слежения
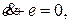 (24)
(24)
которое обеспечивает экспоненциальную сходимость e к нулю.
Применяя тот же самый закон управления ко второму уравнения в переменных состояния, получаем уравнение
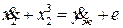 , (25)
, (25)
описывающее внутреннюю динамику и являющееся нелинейным и неавтономным. Учитывая, что ошибка слежения в соответствии с (24) ограничена по величине и скорость желаемой реакции 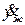 ограничена по условию, мы приходим к выводу, что их разность также ограничена, т.е.
ограничена по условию, мы приходим к выводу, что их разность также ограничена, т.е.
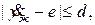 где d положительная постоянная. Отсюда мы делаем вывод, что
где d положительная постоянная. Отсюда мы делаем вывод, что
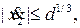 т.к.
т.к. 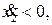 если
если 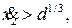 и
и 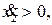 если
если 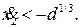 Поэтому выражение (25) дает приемлемый с точки зрения устойчивости внутренней динамики закон управления для системы (21), позволяющий следить за любым желаемым задающим воздействием, производная которого ограничена.
Поэтому выражение (25) дает приемлемый с точки зрения устойчивости внутренней динамики закон управления для системы (21), позволяющий следить за любым желаемым задающим воздействием, производная которого ограничена.
Замечание. Если второе уравнение состояния в (21) заменить на
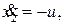
то в результате получим неустойчивую внутреннюю динамику.
Дата добавления: 2015-08-14; просмотров: 1484;
