Линеаризация вход-выход
Рассмотрим задачу слежения применительно к объекту управления, описываемому уравнениями
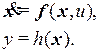 (14)
(14)
Цель управления: добиться, чтобы выход объекта y(t) отслеживал желаемое задающее воздействие yж(t), в то время как все переменные состояния оставались ограниченными по величине.
Рассмотрим объект третьего порядка, описываемый уравнениями
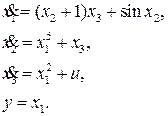 (15)
(15)
Для того, чтобы получить соотношение, непосредственно связывающее выход y(t) и управление u(t), сначала найдем производную от выхода
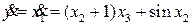 .
.
Как видим, производная явно не связана с управлением u(t). Поэтому еще раз осуществим дифференцирование. Тогда получаем
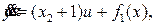 (16)
(16)
где
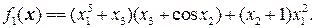 (17)
(17)
Ясно, что (16) дает явную зависимость между y(t) и u(t). Если мы выберем управление в виде
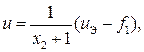 (18)
(18)
где 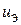 определяется как новое управление, то нелинейности в (16) сокращаются, и мы получаем линейное динамическое уравнение
определяется как новое управление, то нелинейности в (16) сокращаются, и мы получаем линейное динамическое уравнение
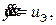
описывающее двойной интегратор. Проектирование следящего регулятора для такого двойного интегратора не представляет трудностей, если использовать методы линейной теории управления. Например, пусть e(t)=yж(t)- y(t) и мы выбрали новое управление как
 (19)
(19)
где 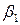 и
и  положительные постоянные. При этом ошибка слежения замкнутой системы управления будет описываться уравнением
положительные постоянные. При этом ошибка слежения замкнутой системы управления будет описываться уравнением
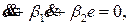 (20)
(20)
которому соответствует применительно к e асимптотически устойчивая динамика, так что ошибка слежения с течением времени затухает до нуля.
Если желаемое задающее воздействие yж(t)представлено постоянным сигналом v(t)= v0 =const, то закон управления 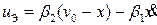 приводит к следующему уравнению замкнутой системы относительно выхода
приводит к следующему уравнению замкнутой системы относительно выхода 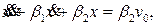 которое обеспечивает при положительных постоянных коэффициентов
которое обеспечивает при положительных постоянных коэффициентов 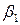 и
и  нулевую установившуюся ошибку воспроизведения постоянного задающего воздействия.
нулевую установившуюся ошибку воспроизведения постоянного задающего воздействия.
Метод линеаризации с обратной связью требует точной модели ОУ с точными производными управляемой величины y=x, что может повлечь за собой проблему робастности. К этому случаю имеется подход к решению задачи робастности, который заключается во введении в закон управления с обратной связью по состоянию интеграла от ошибки
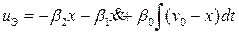 ..
..
Отсюда получаем
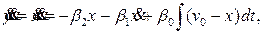
или после дифференцирования
 .
.
Характеристическое уравнение этой системы определяется выражением
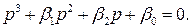
Выбирая коэффициенты данного уравнения так, чтобы все его корни были левыми, мы можем добиться стабилизации системы на уровне 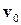 =const и в то же время робастности к постоянному возмущению на входе нелинейного ОУ и к неопределенности параметров модели.
=const и в то же время робастности к постоянному возмущению на входе нелинейного ОУ и к неопределенности параметров модели.
Заметим, что:
- Закон управления (18) определен всюду, кроме особой точки 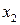 =-1.
=-1.
- Для реализации закона управления требуется измерение всех переменных состояния.
- Данный выше регулятор не гарантирует устойчивости внутренней динамики замкнутой системы, т.е. не гарантирует, что замкнутая система внутренне устойчивая.
Дата добавления: 2015-08-14; просмотров: 1085;
