Линеаризация вход-состояние

Рассмотрим задачу регулирования применительно к объекту с одним входным сигналом u, описываемому нелинейным уравнением

.

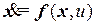Технология линеаризации вход-выход решает эту задачу в два шага:

- Найти преобразование состояния 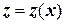и преобразование входного сигнала такие, что динамика нелинейного объекта трансформируется в динамику эквивалентного линейного объекта, описываемого уравнением .

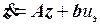- Использовать стандартные методы линейной теории управления, чтобы спроектировать управление u_э.

Пример. Рассмотрим нелинейный объект второго порядка

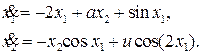(6)

Даже хотя спроектированный линейный регулятор может стабилизировать объект в малой окрестности точки равновесия (0,0), но совершенно не очевидно, что этот регулятор может стабилизировать его в целом. Специфическая трудность заключена в нелинейности, входящей в первое уравнение состояния (6), т.к. она не может быть сокращена с помощью управляющего сигнала u.

Рассмотрим следующее преобразование состояния

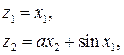(7)

которое преобразует (6) в

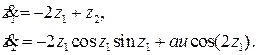(8)

Заметим, что новые уравнения состояния также имеют состояние равновесия в точке (0,0). Теперь нелинейности могут быть сокращены с помощью закона управления в виде

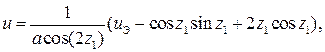(9)

где u_э эквивалентное управление (эквивалентное в том смысле, что определение u_эравносильно определению u и наоборот). Этот закон приводит к линейным уравнениям состояния

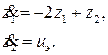(10)

Итак, проблема стабилизации исходного нелинейного объекта, описываемого уравнениями (6) и использующего исходный управляющий сигнал u, с помощью преобразования состояния (7) и преобразования управления (9) сводится к проблеме стабилизации преобразованного объекта, используя новый управляющий сигнал u_э. Теперь рассмотрим преобразованный объект, описываемый уравнениями (10). Нетрудно показать, что он является не только линейным, но и полностью управляемым. Используя хорошо известный линейный закон управления с обратной связью по состоянию 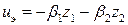, и выбирая коэффициенты 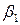=2, 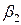=0, так что

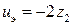, (11)

получаем устойчивый преобразованный объект, описываемый уравнениям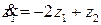и и . В рамках исходного вектора состояния найденный закон управления соответствует исходному управлению

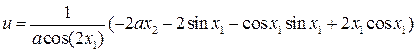. (12)

Исходное состояние xсвязано с z посредством соотношений

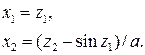(13)

Структурная схема замкнутой системы с полученным выше законом управления представлена на рис. 1.

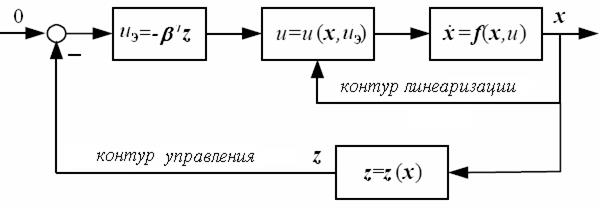
Рис. 1

Замечание. Чтобы обобщить приведенный выше метод нужно ответить на два вопроса:

- Какие классы нелинейных систем могут быть преобразованы в линейные системы?

- Каким путем можно найти соответствующие преобразования для тех систем, которые в принципе могут быть преобразованы в линейные

системы?