Точкой над ней.
ВертиПоложительную начальную фазу откладывают влево от начала координат (см. ток i1 на рис. 5.2), отрицательную – вправо (см. ток i2 на рис. 5.2).tМежду токами i1 и i2 есть сдвиг по фазе. При заданных начальных фазах, фазовый сдвиг остается величиной постоянной.
Угол сдвига фаз напряжения и тока, равный ϕ= ψu – ψi , является важнейшей характеристикой электрической цепи. Если угол ϕ = 0 , напряжение и ток совпадают по фазе.
в). Изображение вращающимися векторами.
Непосредственные математические действия с синусоидальными величинами весьма трудоемки.
Любую синусоиду можно изобразить вектором, вращающимся против часовой стрелки со скоростью ω (рис. 5.3).
Вектор изображают в начальный момент времени (t = 0) . Тогда фаза
колебания (ωt + ψ) = ψ. Длина вектора в масштабе выражает амплитудное
значение величины. Вращающиеся векторы обозначают заглавной буквой с
точкой над ней.
|
Вертикальная проекция вектора определяет мгновенное значение тока
при t = 0: i0 = Imsin ψ.
При вращении с одинаковой скоростью все векторы взаимно неподвижны.
Совокупность векторов, отображающих процесс в цепи, называют векторной диаграммой.
Применение вращающихся векторов позволяет заменить тригонометрические и графические действия над мгновенными значениями действиями над вращающимися векторами. Но векторные диаграммы дают только графическое решение задачи.
г). Изображение комплексными числами.
Для аналитического решения плоскость координат XOY заменим ком-
 |
плексной плоскостью (рис. 5.4).
Так как буквой iв электротехнических дисциплинах обозначают ток, то
мнимую единицу обозначают буквой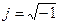 
.
Вектору на комплексной плоскости можно сопоставить комплексное число:
Ỉm = Im e jΨ.
Величину характеризуют модулем комплекса Im, положение на комплексной плоскости – аргументом комплекса ψ.
Такую форму записи комплексного числа в математике называют показательной. Ее можно использовать для умножения и деления комплексных
чисел.
Складывать и вычитать в такой форме записи нельзя, поэтому переходят к так называемой алгебраической форме. Для этого раскладывают вектор Im на проекции по осям координат - действительную I′m и мнимую jI″m :
Im= I′m + jI″m .
Переход от одной формы записи к другой делают по формулам, полученным из решения треугольника (см. рис. 5.4):
, ψ = arctg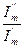 
;
I’m = Im ⋅ cosψ; I”m = Im ⋅ sin ψ.
Метод расчета цепей синусоидального тока при помощи комплексных чисел называется символическим.называют символическим.
3. Действующие и средние значения гармонических величин
1.Действующие значения.
По тепловому действию сравнивают синусоидальный ток с постоянным.
Постоянный ток подбирают таким, чтобы за одинаковое количество времени выделялось одинаковое количество тепла: QI = Qi .
QI =0,24 RI2 T, 
.
Отсюда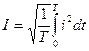 
.
Действующим значением тока считают такой постоянный ток, который
производит тот же тепловой эффект, что и реальный переменный ток.
Примем начальную фазу ψi для простоты равной нулю. Тогда i= Imsinωt .
Действующее значение тока
.
Аналогично 
; 
.
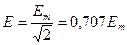Так как действие переменного тока характеризует действующие значения, то на векторных диаграммах принято изображать векторы действующих, а не максимальных значений.
Действующие значения токов и напряжений показывают амперметры и вольтметры электромагнитной и электродинамической систем.
2. Средние значения
В общем случае среднее значение– это среднее значение за период:
.
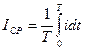Но для синусоидальной величины это выражение равно нулю. Поэтому сред-
нее значение определяют для половины периода:янный ток подбирают таким, чтобы за одинаковое количество
времени выделялось одинаковое количество тепла:
QI
I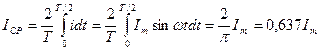 
$
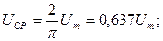ю$$ 0, 
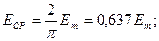707
Дата добавления: 2015-08-20; просмотров: 624;