При синусоидальном

2. Индуктивный элемент.

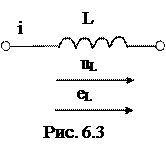
Ток индуктивного элемента (рис. 6.3) создаетмагнитный поток, направленный по оси катушки. Потокосцепление ψ – это произведение числа витков катушки на магнитный поток: ψ =W ⋅Φ.

Одинаковыми буквами могут быть обозначены разные физические величины.

Индуктивный элемент учитывает ЭДС самоиндукции, которая пропорциональна скорости изменения потокосцепленияи мешает этому изменению: 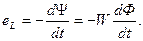итный поток, направ-

= ∫Индуктивная катушка обладает индуктивностью. Индуктивность – это

коэффициент, характеризующий способность тока создавать магнитный по-

ток: 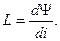Индуктивность измеряют в генри [Гн)] =Ом⋅ с .

Можно записать dψ = Ldi. Тогда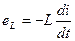

Напряжение на индуктивном элементе u_L = −e_L, т. е.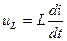

Это закон Ома для мгновенных значений.

Если i= I_msin (ωt + ψ_i ) , напряжение u_L= LωI_mcos(ωt + ψ_i) =

= LωI_m sin (ωt+ ψ_i + π/2).

Отсюда можно сделать выводы:

а). При синусоидальном токе напряжение на индуктивном элементе тоже синусоидально.

б). Напряжение опережает по фазе ток на угол, равный π/2 .

Проиллюстрируем эти выводы графиками: синусоидами (рис. 6.4, а) и

векторной диаграммой (рис. 6.4, б).

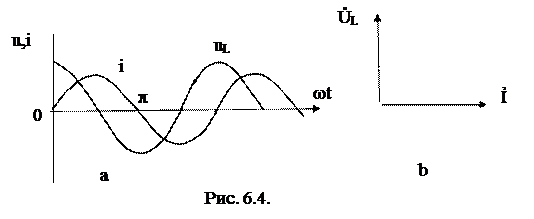Перед знаком синуса записывают максимальное значение, т. е. U_Lm= LωI_m.

Если левую и правую части уравнения разделим на 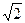, то получим закон Ома для действующих значений: U_L= LωI .

По аналогии с резистором для упрощения расчетов вводят понятие индуктивного сопротивления X_L =L ω, [X_L ]=Ом с 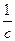= Ом. Тогда U_L= X_L I.

Индуктивное сопротивление – это расчетное понятие, учитывающее ЭДС самоиндукции. Частотная характеристика индуктивного сопротивления представлена на рис. 6.5.

В цепи постоянного тока ω = 0 , поэтому X _L= Lω = 0. Вместо индуктивного элемента в схеме замещения будет закоротка.

Расчеты в цепях синусоидального тока делают символическим методом. Закон Ома для комплексных значений:

Ů_L= j X_L Ỉ= X_L Ỉ e^{j π/2} = X_L Ỉ e^j90º .

Умножение вектора на j или на e^j90º означает его поворот на комплексной плоскости на угол + 90°.

Мгновенная мощность индуктивного элемента:

p = u_L ⋅ i =U_Lm I_m cos (ωt + ψ_i ) sin (ωt + ψ_i ).

Умножим и разделим на 2:

p= 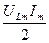2cos(ωt + ψ_i ) sin(ωt + ψ_i )=U_L I sin2(ωt +ψ_i ).

Отсюда следует, что мощность меняется с удвоенной частотой и является знакопеременной.

При p > 0 энергия от источника поступает в индуктивную катушку и запасается в ее магнитном поле. При p < 0 энергия возвращается в сеть.

Активная мощность P= 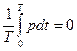,так как мгновенная мощность меняется по синусоидальному закону.

Идеальная индуктивная катушка энергии не потребляет.

Энергия магнитного поля индуктивного элемента:

.

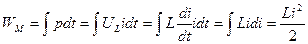3. Идеальный конденсатор либо емкостный элемент

Емкостный элемент (рис. 6.6) обладает емкостью С, которую измеряют в фарадах ( Ф= с/Ом).

измеИИирИИяютИииииш

 

Из курса физики известно, что i =dq/dt, а q =C u_C. Отсда

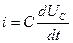. Это закон Ома для мгновенных значений.

Пусть напряжение u_C =U_Сmsin(ωt + ψ_u ).

Тогда i = CωU_Сm cos (ωt + ψ_u ) = CωU_Сm sin(ωt + ψ_u + π/2).

 

Из полученного выражения можно сделать выводы:

а). При синусоидальном токе напряжение на емкостном элементе тоже синусоидально.

б). Напряжение на емкостном элементе отстает по фазе от тока на

угол π/2(90°).

Эти выводы можно проиллюстрировать графиками: синусоидами

(рис. 6.7, а) и векторной диаграммой (рис.6.7, б).

 

 

 

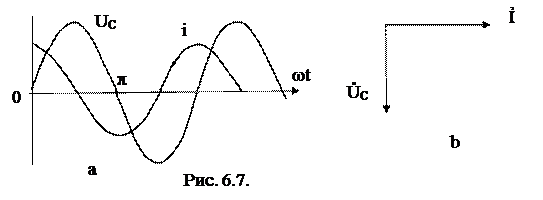Максимальное значение тока I_m = CωU_Cm. Разделив обе части уравне-

ния на 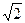, получим закон Ома для действующих значений:

I = CωU_C либо .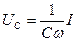

По аналогии с резистором для упрощения расчетов вводят понятие ем-

костного сопротивления Х_C :

. [X_C ] = .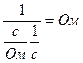

Частотная характеристика емкостного сопроивления приведена на рис. 6.8.

В цепи постоянного тока X_C 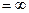, поэтому конденсатор постоянныйток не пропускает.

 

 

Напряжение U_C = X_C I .

Закон Ома для комплексных значений:

Ů_C = − j X_C Ỉ= X_C Ỉ e ^{-j π/2} = X_C Ỉ e ^-j90º

Умножение вектора на –j или на е−^j90° означает его поворот на комплексной плоскости на угол − 90° .

Мгновенная мощность емкостного элемента

p = u_C i =U_Cm I_mcos(ωt + ψ_u )· sin(ωt + ψ_u ) =

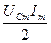= 2cos(ωt + ψ_u ) sin(ωt + ψ_u )=U_C I sin2(ωt +ψ_u ).

Отсюда следуют выводы: мощность меняется с удвоенной частотой и является знакопеременной.

При р >0 энергия от источника поступает в конденсатор и запасается в его электрическом поле. При р <0 энергия возвращается в сеть.

Активная мощность P= 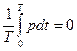, т. к. мгновенная мощность меняется по синусоидальному закону.

Идеальный конденсатор энергии не потребляет. Энергия электрического поля емкостного элемента:

.