Резистор, катушка индуктивности и конденсатор в синусоидальном режиме.
При использовании комплексного метода рассматривают уравнения элементов, связывающие комплексы напряжений и токов.
Синусоидам 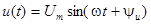 и
и  поставим в соответствие комплексы:
поставим в соответствие комплексы: 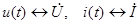 . Учтем, что умножению синусоиды на число соответствует умножение комплекса на то же число, а производной от синусоиды соответствует умножение ее комплекса на
. Учтем, что умножению синусоиды на число соответствует умножение комплекса на то же число, а производной от синусоиды соответствует умножение ее комплекса на 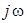 . Из уравнений элементов для мгновенных значений напряжения и тока получим уравнения элементов в комплексах.
. Из уравнений элементов для мгновенных значений напряжения и тока получим уравнения элементов в комплексах.
Уравнение резистора для мгновенных значений напряжения и тока: 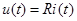 , откуда получаем уравнение резистора в комплексах:
, откуда получаем уравнение резистора в комплексах:
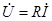 .
.
Рассмотрев модули и аргументы левой и правой частей последнего уравнения, получим:
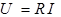 (связь действующих значений напряжения и тока резистора),
(связь действующих значений напряжения и тока резистора),
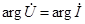 (связь фаз напряжения и тока).
(связь фаз напряжения и тока).
Последнее означает, что фазы напряжения и тока резистора совпадают (рис. 12.1, рис. 12.2).
 Рис. 12.1. Мгновенные значения напряжения
и тока резистора.
Рис. 12.1. Мгновенные значения напряжения
и тока резистора.
|
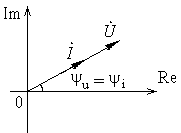 Рис. 12.2. Векторная диаграмма напряжения и тока резистора.
Рис. 12.2. Векторная диаграмма напряжения и тока резистора.
|
Уравнение катушки индуктивности для мгновенных значений напряжения и тока: 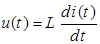 , откуда получаем уравнение катушки индуктивности в комплексах:
, откуда получаем уравнение катушки индуктивности в комплексах:
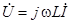 .
.
Рассмотрев модули и аргументы левой и правой частей последнего уравнения, получим (учитывая, что модуль произведения равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей):
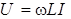 (связь действующих значений напряжения и тока катушки),
(связь действующих значений напряжения и тока катушки),
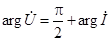 (связь фаз напряжения и тока)
(связь фаз напряжения и тока)
Последнее означает, что фаза напряжения катушки больше фазы ее тока на 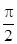 (рис. 12.3, рис. 12.4). Величину
(рис. 12.3, рис. 12.4). Величину 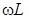 обозначают
обозначают 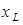 и называют индуктивным сопротивлением. Оно измеряется в омах.
и называют индуктивным сопротивлением. Оно измеряется в омах.
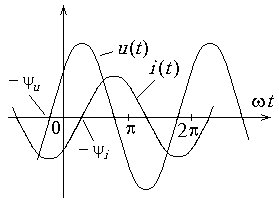 Рис. 12.3. Мгновенные значения напряжения
и тока катушки индуктивности.
Рис. 12.3. Мгновенные значения напряжения
и тока катушки индуктивности.
| 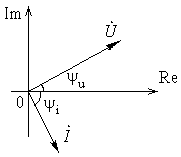 Рис. 12.4. Векторная диаграмма напряжения и тока катушки индуктивности.
Рис. 12.4. Векторная диаграмма напряжения и тока катушки индуктивности.
|
Уравнение конденсатора для мгновенных значений напряжения и тока: 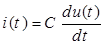 , откуда получаем уравнение конденсатора в комплексах:
, откуда получаем уравнение конденсатора в комплексах:
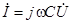 .
.
Рассмотрев модули и аргументы левой и правой частей последнего уравнения, получим:
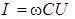 (связь действующих значений напряжения и тока конденсатора),
(связь действующих значений напряжения и тока конденсатора),
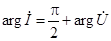 (связь фаз напряжения и тока).
(связь фаз напряжения и тока).
Последнее означает, что фаза тока конденсатора больше фазы его напряжения на 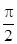 (рис. 12.5, рис. 12.6). Величину
(рис. 12.5, рис. 12.6). Величину 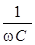 обозначают
обозначают 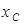 и называют емкостным сопротивлением. Оно измеряется в омах.
и называют емкостным сопротивлением. Оно измеряется в омах.
. 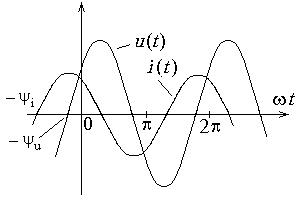 Рис. 12.5. Мгновенные значения напряжения
и тока конденсатора.
Рис. 12.5. Мгновенные значения напряжения
и тока конденсатора.
|
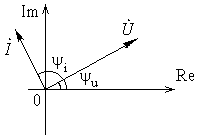 Рис. 12.6. Векторная диаграмма напряжения и тока конденсатора.
Рис. 12.6. Векторная диаграмма напряжения и тока конденсатора.
|
Сводку уравнений этого параграфа можно представить таблицей:
| ур-е для мгновенных значений | ур-е для комплексов | ур-е для действующих значений | ур-е для фаз | |
| Резистор | 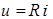
| 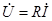
| 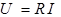
| 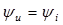
|
| Катушка | 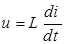
| 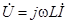
| 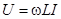
| 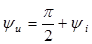
|
| Конденсатор | 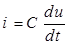
| 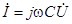
| 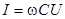
| 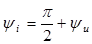
|
Дата добавления: 2015-08-11; просмотров: 1356;
