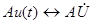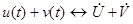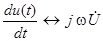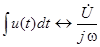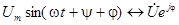Комплексный метод расчета синусоидальных режимов эл. цепей.

Синусоидальным режимом эл. цепи называется такой режим, при котором все напряжения и токи цепи изменяются по синусоидальному закону с одной и той же частотой.

Синусоидальные напряжения и токи широко применяются в основном по следующим причинам:

1. Они легко получаются с помощью различных генераторов.

2. Они легко преобразуются трансформаторами.

3. С их помощью легко создаются вращающиеся и бегущие магнитные поля, используемые в электродвигателях.

4. Сложением синусоидальных колебаний можно получать различные несинусоидальные напряжения и токи.

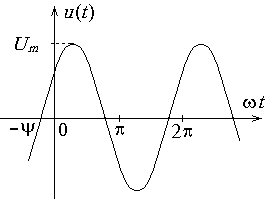Рис. 1.11.

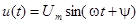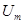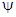Рассмотрим синусоидальное напряжение . Его характеризуют три параметра: амплитуда , круговая частота и начальная фаза (рис. 11.1). Амплитудные значения в электротехнике обозначаются большими буквами с индексом m.

К характеристикам синусоиды 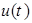относятся также действующее значение U, циклическая частота 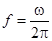(т.е. количество колебаний в секунду), и период .

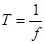Синусоидальный ток 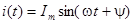характеризуется аналогичными параметрами .

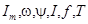Для любой синусоиды действующее значение и амплитуда связаны коэффициентом : .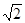

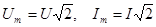Состояние эл. цепей в синусоидальных режимах можно описывать, пользуясь функциями времени. Однако, это громоздко и трудоемко. Поэтому для расчетов синусоидальных режимов применяется комплексный метод. Он позволяет заменить дифференциальные и интегральные уравнения элементов эл. цепи алгебраическими, а также весьма наглядно представить синусоиды в виде векторов на векторных диаграммах.

Основа метода состоит в том, что каждой синусоиде ставится в соответствие комплексное число, называемое комплексом. Такое соответствие взаимно однозначно. Оно определяется правилом:

,

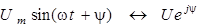где 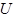– действующее значение синусоиды, y – начальная фаза синусоиды, 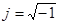– мнимая единица (в электротехнике она обозначается этой буквой). Информация о частоте в комплекс не входит и должна учитываться отдельно. Комплексы обозначаются большими буквами с точкой: 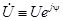, или подчеркнутой большой буквой: .

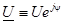Примеры: ,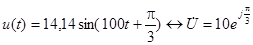

.

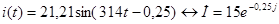Общая схема метода:

1. Переход от синусоид к комплексам.

2. Решение задачи в комплексах.

3. Переход от комплексов к синусоидам (если это нужно).

Рассмотрим произвольные синусоиды 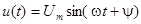и 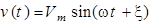, их комплексы 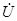и 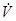, а также произвольное действительное число А. Операции на множестве синусоид и операции на множестве комплексов обладают следующим соответствием:

Такое соответствие операций позволяет рассматривать множество синусоид и множество комплексных чисел как по существу один и тот же математический объект. Доказательство несложно и опирается на свойства синусоид и комплексных чисел.

Комплексы изображаются векторами на плоскости согласно обычным правилам, принятым для комплексных чисел. В электротехнике такие рисунки называются векторными диаграммами.

Стрелки на векторной диаграмме - это изображения синусоид, а стрелки на схемах эл. цепи - это направления вычисления напряжений и токов!

Благодаря линейности соответствия синусоид и комплексов законы Кирхгофа, а также все другие свойства и методы расчета линейных эл. цепей при переходе к комплексам сохраняются.

Замечание 1: В качестве модулей комплексов мы приняли действующие значения синусоид: 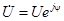. Такие комплексы называются комплексами действующих значений. Однако, иногда бывает удобно принять в качестве модулей комплексов амплитудные значения синусоид: 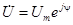. Такие комплексы называются комплексными амплитудами.

Замечание 2: Любую синусоиду можно представить также в виде синус- и косинус-составляющих:

,

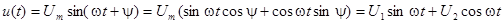где 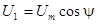, 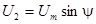. При этом , .

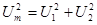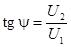Так как для комплексных амплитуд 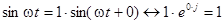, , 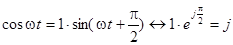то представление синусоиды в виде синус- и косинус-составляющих позволяет поставить ей в соответствие комплексную амплитуду в алгебраической форме:

.

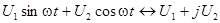Замечание 3: Комплексный метод применяется не только в электротехнике, но везде, где исследуются синусоидальные колебания.