Мощность двухполюсника в синусоидальном режиме

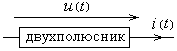Рис. 14.1.

Рассмотрим двухполюсник в синусоидальном режиме. Будем иметь в виду потребляемую мощность, поэтому стрелки напряжения и тока направим в одну сторону (рис. 14.1)

Пусть .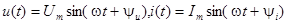

Вычислим активную мощность, потребляемую двухполюсником (здесь 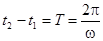– период u(t) и i(t)):

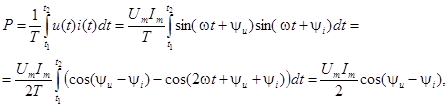
так как .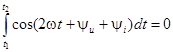

Учитывая, что 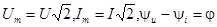, где U и I – действующие значения напряжения и тока, j – сдвиг фаз между напряжением и током, получим:

.

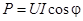Число 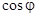называется коэффициентом мощности. При использовании мощных электромагнитных устройств стараются увеличить 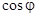,сделать его как можно ближе к единице, потому что при 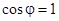достигается максимальная активная мощность, возможная при заданных значениях напряжения и тока. Эту мощность называют полной мощностью и обозначают буквой S :

.

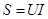Полная мощность измеряется в вольт-амперах: ВА.

С другой стороны, при заданном напряжении и заданной активной мощности условие 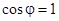соответствует минимальному значению тока в линии электропередач, соединяющей источник электроэнергии с нагрузкой. Это обеспечивает минимум потерь энергии в проводах линии.

Очень важную роль в энергетике играют трансформаторы и асинхронные электродвигатели. Они имеют максимальный 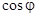при максимальной нагрузке. Поэтому полная загрузка используемого оборудования представляет один из основных способов повышения коэффициента мощности. Второй способ – применение компенсаторов реактивной мощности (конденсаторов и синхронных электрических машин).

Реактивная мощность обозначается буквой Q и определяется формулой

.

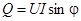Реактивная мощность измеряется в вольт-амперах реактивных: ВАр. Она может быть измерена приборами. По значениям активной и реактивной мощности можно судить о значении коэффициента мощности и об эффективности использования оборудования. Для стимулирования повышения 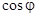тарифы на электроэнергию могут зависеть от значения реактивной мощности.

Выражения для полной, активной и реактивной мощности можно получить также из комплексов напряжения и тока двухполюсника. При этом вводится понятие комплексной мощности :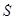

,

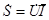где 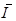– число, комплексно сопряженное к комплексу тока.

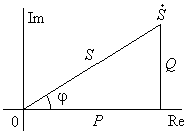Рис. 14.2.

Получим связь :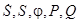

,

.

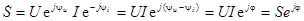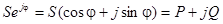Итак, .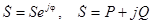

Полученные зависимости изображают на комплексной плоскости в виде “треугольника мощностей” (рис. 14.2).