Соединение трехфазного источника напряжения и нагрузки звездой

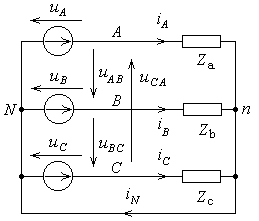Рис. 18.1.

Трехфазный источник напряжения и трехфазная нагрузка соединяются звездой или треугольником. Соединение звездой показано на рис. 18.1.

Точка соединения всех фаз источника напряжения называется нейтральной (или нулевой) точкой источника и обозначается N. Точка соединения всех фаз нагрузки называется нейтральной (или нулевой) точкой нагрузки и обозначается n.

Провод, соединяющий нейтральные точки источника и нагрузки, называется нейтральным (или нулевым). Он обеспечивает независимую работу фаз цепи. То есть, если в какой-то одной фазе произойдут изменения режима работы, две другие фазы этого "не заметят".

Ток в нейтральном проводе обычно бывает меньше, чем в линейных проводах, поэтому нейтральный провод часто делают тоньше линейных проводов. При симметричной нагрузке ток в нейтральном проводе равен нулю, поэтому в таком случае (например, при подключении трехфазных двигателей или печей) нейтральный провод вообще не используют.

Нейтральный провод часто заземляют и соединяют с ним корпуса электрооборудования (защитное зануление).

Напряжения 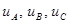называются фазными, т.к. это напряжения фаз источника и нагрузки. Напряжения 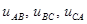называются линейными, т.к. это напряжения между линейными проводами. Токи 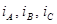являются одновременно фазными и линейными, т.к. это одновременно токи фаз источника и нагрузки, а также токи в линейных проводах.

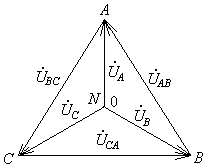Рис. 18.2.

Рассмотрим уравнения, описывающие состояние рассматриваемой цепи. Согласно 2-му закону Кирхгофа:

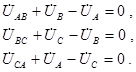
Эту связь между фазными и линейными напряжениями можно изобразить на векторной диаграмме (рис. 18.2). Из этого рисунка видна связь действующих значений фазных и линейных напряжений:

.

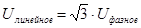На трехфазных векторных диаграммах часто ставят буквы, соответствующие точкам схемы эл. цепи, например, A, B, C, N (рис. 18.2). Эти буквы надо понимать как обозначение точек комплексной плоскости, соответствующих изменяющимся по синусоидальному закону электрическим потенциалам точек цепи A, B, C, N.

В нашем случае j_N = 0, j_A = u_A, j_B = u_B, j_C = u_C, поэтому уравнение 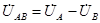соответствует уравнению u_AB = j_A - j_B. Стрелка напряжения 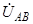на векторной диаграмме направлена от точки В к точке А, потому что она получается как разность векторов 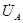и .

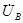Обратим внимание на то, что в соответствии с тем же уравнением u_AB = j_A - j_B стрелка того же напряжения u_AB на схеме цепи по определению направлена от точки А к точке В.Это различие получается оттого, что стрелки на схеме обозначают направление вычисления напряжений и токов, а стрелки на векторных диаграммах - это изображение соответствующих синусоид на комплексной плоскости.

Согласно 1-му закону Кирхгофа 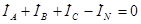, то есть ток в нейтральном проводе равен сумме токов в линейных проводах. Эта связь токов показана на векторных диаграммах рис. 18.3–18.8.

Согласно уравнениям фаз нагрузки (по закону Ома):

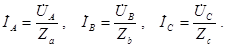
Такая связь напряжений и токов для случаев различных нагрузок показана на рис. 18.3 –18.8.

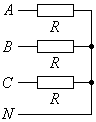Рис. 18.3.	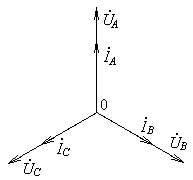Рис. 18.4.
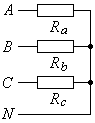Рис. 18.5.	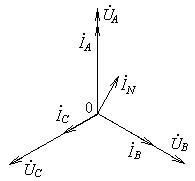Рис. 18.6.

Векторные диаграммы токов рассмотрим на примерах некоторых конкретных типов нагрузки.

В простейшем случае симметричной резистивной нагрузки (то есть, когда все три фазы нагрузки – это одинаковые резисторы, как в опыте №1 лабораторной работы №4, рис. 18.3) векторная диаграмма токов и фазных напряжений выглядит так, как показано на рис. 18.4. Ток и напряжение каждого элемента нагрузки совпадают по фазе, поэтому соответствующие векторы направлены в одну сторону. Действующие значения всех трех токов одинаковы, поэтому векторы токов имеют одинаковую длину. Сумма фазных токов равна нулю, поэтому ток в нейтральном проводе тоже равен нулю и не показан на диаграмме.

Для несимметричной резистивной нагрузки (когда все три фазы нагрузки – это резисторы, но с разным сопротивлением, рис. 18.5) векторная диаграмма показана на рис. 18.6. Резистивную нагрузку также называют активной. Вектор, изображающий ток в нейтральном проводе, равен сумме векторов, изображающих фазные токи.

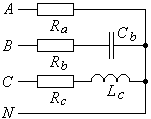Рис. 18.7.

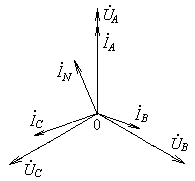Рис. 18.8.

Для несимметричной нагрузки, состоящей из резистора в фазе a, активно-емкостного элемента в фазе b и активно-индуктивного элемента в фазе c (рис. 18.7), диаграмма показана на рис. 18.8. Основное отличие от рис. 18.6 состоит в сдвигах фаз фазных токов относительно фазных напряжений.

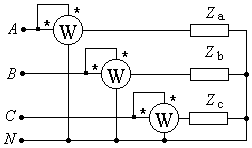Рис. 18.6.

Типичные виды нагрузки трехфазной цепи – это активная и активно-индуктивная. В опыте №2 лабораторной работы №3 параллельное соединение резистора и конденсатора представляет собой активно-емкостную нагрузку.

Активная мощность трехфазной нагрузки равна сумме мощностей фаз: 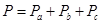. Мощности фаз можно измерить, включив ваттметры по схеме рис. 18.6. Каждый ваттметр включен на фазное напряжение и фазный ток соответствующей фазы нагрузки. В случае симметричной нагрузки можно измерить мощность только одной фазы и умножить ее на три.