Смешанное соединение резистора, катушки индуктивности и конденсатора.
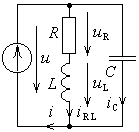 Рис. 16.1.
Рис. 16.1.
|
Рассмотрим двухполюсник, состоящий из смешанного соединения резистора, катушки индуктивности и конденсатора (рис. 16.1). Он подключен к источнику синусоидального напряжения, амплитуда которого постоянна.
Будем понимать эту цепь как модель энергетической системы, состоящей из источника напряжения е, соединенного линией электропередач с нагрузкой в виде последовательно соединенных резистора R и катушки индуктивности L. Такая модель выбрана, потому что в энергетике большую долю нагрузки составляют электродвигатели и трансформаторы, которые необратимо отбирают электрическую энергию из сети (так, как это делает резистор), а также периодически запасают энергию в магнитном поле своих индуктивностей и отдают ее обратно в цепь (так, как это делает катушка индуктивности).
Емкость С рассчитаем так, чтобы ток I в линии электропередач был минимальным. Это позволит свести к минимуму потери энергии в проводах линии электропередач, соединяющей источник энергии и нагрузку (см. п.14, а также лабораторную работу №3 по общей электротехнике). Такой режим часто называют компенсацией реактивной мощности нагрузки.
Согласно определению полной проводимости двухполюсника (см. п.13),
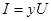 ,
,
то есть, при заданном напряжении U минимум тока I достигается при минимуме полной проводимости y. Найдем эту проводимость, используя эквивалентные преобразования сопротивлений.
Комплексное сопротивление последовательно включенных резистора и катушки будет равно сумме комплексных сопротивлений этих элементов (см. п. 13):
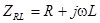 .
.
Комплексная проводимость ветви с резистором и катушкой будет обратна к комплексному сопротивлению этой ветви:
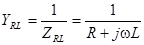 .
.
При параллельном соединении проводимости складываются, поэтому
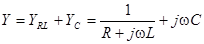 .
.
Чтобы найти у, удобно выделить действительную и мнимую часть Y. Сделаем это, умножив числитель и знаменатель дроби на выражение, комплексно сопряженное знаменателю:
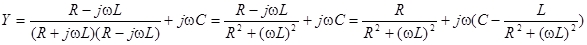 .
.
Используем принятые в электротехнике обозначения: 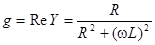 – активная проводимость двухполюсника,
– активная проводимость двухполюсника, 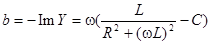 – реактивная проводимость двухполюсника (см. п.13).
– реактивная проводимость двухполюсника (см. п.13).
Согласно определению полной проводимости 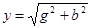 (см. п.13).
(см. п.13).
Так как g не зависит от емкости конденсатора С, то у как функция от С достигает минимума при 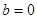 . Отсюда получаем формулу для емкости конденсатора:
. Отсюда получаем формулу для емкости конденсатора:
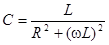 .
.
Обратим внимание на то, что 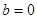 – это условие фазового резонанса (см. п.15). Так как при этом сопротивление двухполюсника максимально, то это в данном случае фазовый резонанс совпадает с резонансом токов.
– это условие фазового резонанса (см. п.15). Так как при этом сопротивление двухполюсника максимально, то это в данном случае фазовый резонанс совпадает с резонансом токов.
Построим векторную диаграмму напряжений и токов. Вначале нарисуем комплекс напряжения 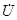 (рис. 16.2). Его фазу будем считать нулевой, поэтому вектор
(рис. 16.2). Его фазу будем считать нулевой, поэтому вектор 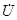 направим вдоль действительной оси. Затем найдем сдвиг фаз между напряжением и током ветви RL (см. пример п. 13):
направим вдоль действительной оси. Затем найдем сдвиг фаз между напряжением и током ветви RL (см. пример п. 13): 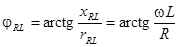 - это угол между действительной осью и вектором, изображающим комплекс тока ветви RL.
- это угол между действительной осью и вектором, изображающим комплекс тока ветви RL.
Найдем значение тока ветви RL: 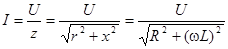 - это длина вектора, изображающего комплекс тока ветви RL (в некотором графическом масштабе).
- это длина вектора, изображающего комплекс тока ветви RL (в некотором графическом масштабе).
Нарисуем на диаграмме комплекс тока ветви RL (рис. 16.2).
Ток всего двухполюсника 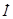 равен сумме тока ветви RL
равен сумме тока ветви RL 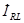 и тока конденсатора
и тока конденсатора 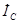 :
: 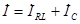 . Ток конденсатора сдвинут по фазе относительно напряжения на
. Ток конденсатора сдвинут по фазе относительно напряжения на 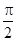 . Нарисуем комплекс тока конденсатора и сложим его с комплексом тока ветви RL, получим ток
. Нарисуем комплекс тока конденсатора и сложим его с комплексом тока ветви RL, получим ток 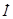 (рис. 16.3).
(рис. 16.3).
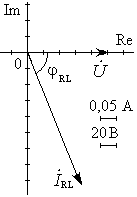 Рис. 16.2.
Напряжение и ток ветви RL.
Рис. 16.2.
Напряжение и ток ветви RL.
| 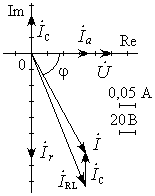 Рис. 16.3. Векторная диаграмма напряжения и тока смешанного соединения RLC (частичная компенсация реактивного тока).
Рис. 16.3. Векторная диаграмма напряжения и тока смешанного соединения RLC (частичная компенсация реактивного тока).
| 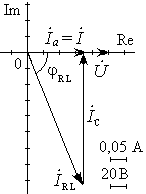 Рис. 16.4. Полная компенсация реактивного тока (резонанс токов).
Рис. 16.4. Полная компенсация реактивного тока (резонанс токов).
|
На рис. 16.3 видно, что наличие в цепи тока конденсатора 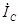 приводит к уменьшению тока в линии электропередач
приводит к уменьшению тока в линии электропередач 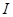 по сравнению с током нагрузки
по сравнению с током нагрузки 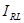 . На рис. 16.4 показан случай, когда ток
. На рис. 16.4 показан случай, когда ток 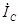 подобран так, что он обеспечивает минимум тока
подобран так, что он обеспечивает минимум тока 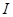 .
.
Дата добавления: 2015-08-11; просмотров: 1640;
