Комплексные числа.
Введение.
Комплексные числа имеют три формы записи. Алгебраическая форма представляет число в виде 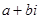 ; здесь a и b – действительные числа, i – число иного рода, называемое мнимой единицей. Основное свойство числа i состоит в том, что его квадрат равен минус единице:
; здесь a и b – действительные числа, i – число иного рода, называемое мнимой единицей. Основное свойство числа i состоит в том, что его квадрат равен минус единице: 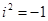 . Числа вида
. Числа вида 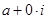 являются действительными. Числа вида
являются действительными. Числа вида 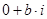 называются мнимыми.
называются мнимыми.
Обозначим число 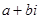 буквой z . Число a называется действительной частью числа z, число b – мнимой частью числа z . Коротко это можно записать так:
буквой z . Число a называется действительной частью числа z, число b – мнимой частью числа z . Коротко это можно записать так: 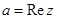 ,
, 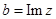 , где Re и Im – принятые в математике обозначения действительной и мнимой части комплексного числа (по-английски Real – действительный, Imaginary – мнимый).
, где Re и Im – принятые в математике обозначения действительной и мнимой части комплексного числа (по-английски Real – действительный, Imaginary – мнимый).
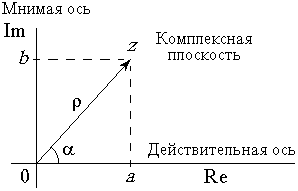 Рис. 7.1.
Рис. 7.1.
|
Число z можно понимать как упорядоченную пару действительных чисел 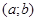 . Поэтому его можно изобразить точкой на плоскости. Действительная часть откладывается по оси абсцисс, а мнимая часть – по оси ординат (рис. 7.1).
. Поэтому его можно изобразить точкой на плоскости. Действительная часть откладывается по оси абсцисс, а мнимая часть – по оси ординат (рис. 7.1).
Комплексное число чаще изображают не точкой, а вектором, начало которого совпадает с началом координат комплексной плоскости, а конец имеет декартовы координаты 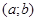 . Если такой вектор перенести параллельно самому себе, он также будет изображать то же самое число.
. Если такой вектор перенести параллельно самому себе, он также будет изображать то же самое число.
Точку на плоскости можно рассматривать и в полярных координатах 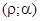 , где r – расстояние от точки до начала координат, a – угол между отрезком, соединяющим точку с началом координат, и осью абсцисс (рис. 7.1).
, где r – расстояние от точки до начала координат, a – угол между отрезком, соединяющим точку с началом координат, и осью абсцисс (рис. 7.1).
Число r называется модулем числа z , число a называется аргументом (или фазой) числа z . Коротко это обозначается так: 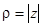 ,
, 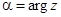 .
.
Из рис. 7.1 видно, что
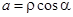 ,
, 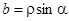 , (7.1)
, (7.1)
поэтому комплексное число z можно представить в виде
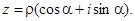
Такая форма представления комплексного числа называется тригонометрической.
Отметим, что 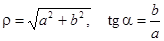 . (7.2)
. (7.2)
Формулы 7.1 определяют переход от тригонометрической формы комплексного числа к алгебраической, формулы 7.2 – от алгебраической к тригонометрической. При этом a лежит в пределах от –p до p и вычисляется с учетом знаков a и b :
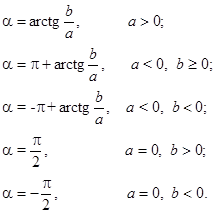
Для числа 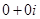 аргумент не определен.
аргумент не определен.
Формула Эйлера 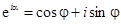 позволяет ввести показательную форму комплексного числа:
позволяет ввести показательную форму комплексного числа: 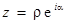 . Модуль r и фаза a имеют тот же смысл, что и для тригонометрической формы комплексного числа.
. Модуль r и фаза a имеют тот же смысл, что и для тригонометрической формы комплексного числа.
Формулу Эйлера можно понимать как определение экспоненты с мнимым показателем: 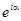 – это такое комплексное число, действительная часть которого равна
– это такое комплексное число, действительная часть которого равна 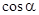 , а мнимая равна
, а мнимая равна 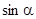 . Более корректно функция
. Более корректно функция 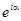 определяется как сумма ряда
определяется как сумма ряда 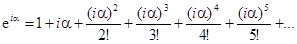 .
.
Учитывая, что 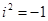 и сгруппировав отдельно действительные и мнимые слагаемые этого ряда, получим ряды для косинуса и синуса, что и доказывает формулу Эйлера (строго говоря, такая перегруппировка слагаемых нуждается в обосновании, но мы законность этого действия примем без доказательства):
и сгруппировав отдельно действительные и мнимые слагаемые этого ряда, получим ряды для косинуса и синуса, что и доказывает формулу Эйлера (строго говоря, такая перегруппировка слагаемых нуждается в обосновании, но мы законность этого действия примем без доказательства):
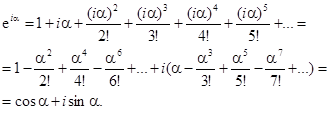
Для экспоненты с мнимым показателем, так же как и для экспоненты с действительным показателем, справедливо свойство: произведение двух экспонент равно экспоненте, показатель которой равен сумме показателей сомножителей:
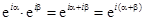 .
.
Сложение комплексных чисел
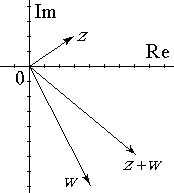 Рис. 7.2.
Рис. 7.2.
|
Суммой комплексных чисел 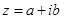 и
и 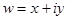 называется комплексное число
называется комплексное число 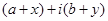 .
.
То есть, действительная часть суммы – это сумма действительных частей слагаемых, а мнимая часть суммы – это сумма мнимых частей слагаемых.
Например, если 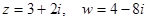 , то
, то 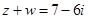 .
.
На комплексной плоскости сложению комплексных чисел соответствует сложение векторов (рис. 7.2).
Сложение чисел в показательной и тригонометрической форме неудобно. Чтобы сделать это, нужно сначала перевести оба числа в алгебраическую форму, сложить их, а затем перевести результат в нужную форму.
Например,
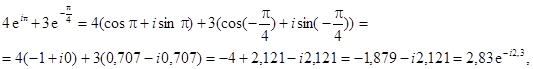
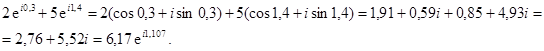
Умножение комплексных чисел
Умножение комплексных чисел в алгебраической форме выполняется по тем же правилам, что и умножение действительных чисел. Единственное различие в том, что 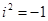 :
:
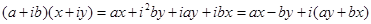 .
.
Например, 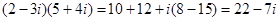 .
.
Умножение комплексных чисел в показательной форме выполняется еще проще. Пусть 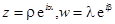 , тогда
, тогда
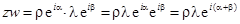 ,
,
то есть, при умножении комплексных чисел модуль произведения равен произведению модулей сомножителей, а аргумент произведения равен сумме аргументов сомножителей.
Например, 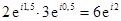 ;
; 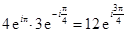 .
.
С помощью формулы Эйлера из правила умножения комплексных чисел в показательной форме может быть получено правило умножения комплексных чисел в тригонометрической форме. Оно такое же, как для чисел в показательной форме.
Замечание 1: Мнимая единица может записываться как перед действительным множителем, так и после него: 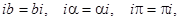 и т.д. Эти выражения равны вследствие того что произведение любых двух комплексных чисел коммутативно, т.е не зависит от порядка сомножителей.
и т.д. Эти выражения равны вследствие того что произведение любых двух комплексных чисел коммутативно, т.е не зависит от порядка сомножителей.
Замечание 2: Аргументы комплексных чисел могут выражаться как в радианах (то есть просто в числах), так и в градусах. Запись аргументов комплексных чисел в радианах, как правило, применяется в математике и физике; запись в градусах – в технических науках и инженерных расчетах.
Умножению комплексного числа z на число 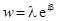 соответсвует растяжение вектора, изображающего число z, в
соответсвует растяжение вектора, изображающего число z, в 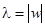 раз и поворот его на угол
раз и поворот его на угол 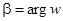 . Это следует из описанных выше правил умножения.
. Это следует из описанных выше правил умножения.
Деление комплексных чисел
Проще всего делить числа в показательной и тригонометрической форме. При этом модуль частного равен отношению модулей делимого и делителя, аргумент частного равен разности аргументов делимого и делителя. Это правило прямо следует из правил умножения.
Пусть 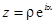 ,
, 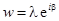 , тогда
, тогда 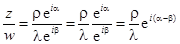 .
.
Например, 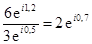 .
.
Чтобы разделить комплексное число в алгебраической форме на действительное число, нужно разделить отдельно действительную и мнимую часть. Пусть 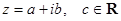 , тогда
, тогда 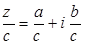 . Например:
. Например: 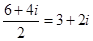 .
.
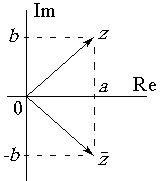 Рис. 7.3.
Рис. 7.3.
|
Деление комплексного числа в алгебраической форме на комплексное число в алгебраической форме сводят к делению комплексного числа на действительное. Это делают путем умножения числителя и знаменателя на число, комплексно сопряженное знаменателю.
Комплексно сопряженное число обозначается звездочкой или чертой наверху, например, 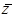 . Комплексно сопряженные числа имеют одну и ту же действительную часть и противоположные мнимые части:
. Комплексно сопряженные числа имеют одну и ту же действительную часть и противоположные мнимые части: 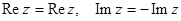 . На комплексной плоскости комплексно сопряженные числа расположены симметрично относительно действительной оси (рис. 7.3). Произведение числа на его сопряженное равно квадрату его модуля, это всегда неотрицательное действительное число:
. На комплексной плоскости комплексно сопряженные числа расположены симметрично относительно действительной оси (рис. 7.3). Произведение числа на его сопряженное равно квадрату его модуля, это всегда неотрицательное действительное число: 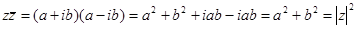 .
.
Итак, разделим два числа в алгебраической форме. Пусть 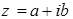 ,
, 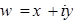 .
.
Тогда 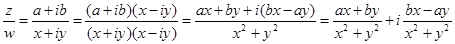 .
.
Например, 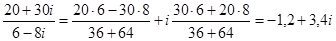 .
.
Дата добавления: 2015-08-11; просмотров: 1498;
