ЛЕКЦИЯ 8. АНАЛИЗ ЦЕПИ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ПРИЕМНИКОВ

Активная проводимость G является действительной составляющей

комплексной проводимости :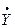

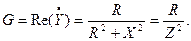
Реактивная проводимость В является мнимой составляющей комплекс-

ной проводимости :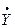

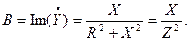
4. Резонанс токов

Этот режим наблюдается в цепи с параллельным соединением индук-

тивных катушек и конденсаторов. Условие резонанса токов: входная реак-

тивная проводимость В = 0.

Рассмотрим резонансный режим для цепи, схема замещения которой изображена на рис. 8.6.

Так как B = B_L − B_C = 0 , то B_L = B_C .

Индуктивная проводимость .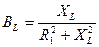

Емкостная проводимость .

При резонансе полная проводимость

.

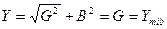Ток I = Y U = G U = I_min.

Графики зависимостей Y(ω) и I (ω) изображены соответственнона рис. 8.7. a и рис. 8.7.b

Построим векторную диаграмму. Величины, общей для схемы рис. 8.6, нет. Поэтому сначала построим векторные диаграммы для отдельных ветвей, в которых элементы соединены последовательно (рис. 8.8, а и б).

Если ветвь имеет активно-индуктивный характер, то вектор напряже-

ния Ů опережает вектор тока Ỉ₁ на острый угол φ₁ =arctg X_L /R₁ .

Если ветвь имеет активно-емкостный характер, то вектор напряжения

Ů отстает от вектора тока Ỉ₂ на острый угол φ₂ =arctg X_C /R₂ .

Поскольку вектор напряжения Ů одинаков, поэтому можно построить объединенную векторную диаграмму (рис. 8.9).

Входной ток Ỉ совпадает по фазе с входным напряжением Ů.

Резонанс токов находит применение, например, в качестве фильтра-пробки для определенной частоты, для улучшения коэффициента мощности.

ЛЕКЦИЯ 9

РАСЧЕТ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА

План лекции

1. Цепь с одним источником энергии

2. Мощности в цепях синусоидального тока.

3. Понятие о коэффициенте мощности и способах его улучшения

Для расчета цепей синусоидального тока применяют те же методы, что и для расчета цепей постоянного тока. Но их можно использовать только для комплексных значений. Рассмотрим несколько примеров.

1. Цепь с одним источником энергии

Пример. Вычислить токи в цепи с одним источником энергии, схема замещения которой изображена на рис. 9.1, если известны значения Ů, R, R₁, X _L, X_L1, X_C . Построить векторную диаграмму.

Решение

1. Выявим узлы (с и d), ветви, зададим направления токов.

2. Для расчета токов в схеме с одним источником энергии рационально использовать метод эквивалентных преобразований.

Эквивалентное комплексное сопротивление

.

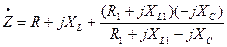3. Комплекс тока в свернутой схеме найдем по закону Ома: .