ЛЕКЦИЯ 9. РАСЧЕТ ЦЕПЕЙ СИНУСОИДАЛЬНОГО ТОКА

4. Токи в пассивных параллельных ветвях вычислим по формулам:

; .

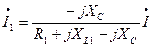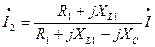5. Действующие значения токов являются модулями комплексных значений.

Векторную диаграмму (рис. 9.2) строим в соответствии с алгоритмом:

а). Построим вектор напряжения между двумя узлами Ů_{cd .}

б). Построим векторы токов в пассивных параллельных ветвях Ỉ₁ и Ỉ₂.

Первая ветвь имеет активно-индуктивный характер, поэтому вектор тока Ỉ₁

отстает от вектора напряжения Ů_cd на угол φ₁ =arctg X_L1 /R_{1 ,} являющийся

аргументом комплексного сопротивления первой пассивной ветви Ż₁ .

Вторая ветвь имеет емкостный характер. Поэтому вектор тока Ỉ₂ опережает вектор напряжения Ů_cd на угол 90° .

в). Cтроим вектор тока Ỉ, равный геометрической сумме векторов токов Ỉ₁ и Ỉ₂.

г). Вектор входного напряжения складывается из векторов трех напряжений:

Ů_ab , Ů_bc и Ů_cd . К вектору Ů_cd прибавляем вектор напряжения Ů_ab . Между точками а и b в схеме находится резистор с сопротивлением R. Напряжение на нем совпадает по фазе стоком Ỉ, поэтому вектор Ů_ab параллелен вектору тока Ỉ. Напряжение на индуктивном элементе опережает ток на ° 90 , поэтому вектор Ů_bc перпендикулярен вектору тока Ỉ.

2. Мощности в цепях синусоидального тока

В цепях синусоидального тока существуют мгновенная р, активная Р, реактивная Q и полная S мощности.

При расчетах удобно пользоваться понятием комплексной мощности

S = Ů I^*,

где Ů =Ue ^jψu – комплекс напряжения

I^*= Ie^{− jψi} – комплекс, сопряженный комплексу тока.

Подставив значения Ů и I^* в соотношение комплексной мощности, получим

S =U e ^jψu ⋅ I e^{− jψi} =U ⋅ I e ^{j(ψu −ψi )} =U ⋅ I e ^jϕ =UI cosϕ + jUI sin ϕ = P + jQ.

Активная мощность является действительной составляющей комплексной мощности: P = Re (S) = Re {Ů I^*}.

Реактивная мощность является мнимой составляющей комплексной

мощности: Q = Im (S) = Im {Ů I^*}.

Для измерения активной (потребляемой) мощности служат ваттметры, представляющие собой сочетание амперметра и вольтметра. Два зажима ваттметра (один – обмотки напряжения и один – обмотки тока) обозначают одинаковыми знаками, обычно звездочками. Угол сдвига фаз между напряжением на ваттметре и током в нем соответствует одинаковым положительным направлениям Ů_W и Ỉ_W относительно зажимов, отмеченных звездочками.

Для указанных (рис. 9.3, а) направлений напряжения и тока:

P =Re (S) =Re {Ů_ab I^*} или P = U_ab I cos(Ů_ab ^ Ỉ).

Для схемы, приведенной на (рис. 9.3, б), активная мощность:

P =Re (S) =Re {Ů_ab (- Ỉ)} = U_ab I cos{Ů_ab ^ (-Ỉ)}.

Для схемы рис. 9.3, в:

P =Re (S) =Re {(-Ů_ab) I^*} = U_ab I cos{(-Ů_ab )^ Ỉ}.

3. Понятие «коэффициент мощности» и способы его улучшения

Потребляемой полезной мощностью является активная мощность Р. Разделение полной мощности на активную и реактивную зависит от угла сдвига фаз ϕ между напряжением и током. Величина угла ϕ определяется соотношением между активным и реактивным сопротивлениям потребителя. Активная мощность P = S cosϕ.

Косинус угла ϕ называют коэффициентом мощности, потому что от его величины зависит, какая доля полной мощности потребляется. Под улучшением коэффициента мощности понимают увеличение cosϕ, т. е. уменьшение угла ϕ. Если увеличение потребляемой мощности не требуется, то увеличение cosϕ необходимо для уменьшения тока. Полезную работу совершает только активная составляющая тока Ia(проекциюя вектора тока Ỉ на вектор напряжения) - рис. 9.4.

Но в цепи циркулирует ток I > Ia , поэтому нужно делать большее сечение проводов линии передачи, обмоток генераторов, трансформаторов и других электрических машин. Кроме того, увеличиваются потери на нагрев проводников (RI²).

ЛЕКЦКоэффициент мощности определяется становлением правительства (~0,92). В целях стимулирования повышения коэффициента мощности промышленные предприятия оплачивают электрическую энергию по дифференцированному тарифу. Чем ниже cosϕ, тем дороже электрическая энергия обходится предприятию.

Способы улучшения cosϕ.

Коэффициент мощност

Cos φ = .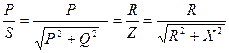

Очевидно, что для повышения cosϕ нужно увеличивать активную мощность и активное сопротивление либо уменьшать реактивную мощность и реактивное сопротивление. Естественный путь – увеличение активной мощности, повышение загрузки оборудования.

Коэффициент мощности асинхронных двигателей и трансформаторов при номинальной нагрузке бывает порядка 0,8–0,9. Асинхронные двигатели и

трансформаторы, работающие недогруженными, снижают cosϕ в сетях.

Искусственный путь – уменьшение реактивной мощности, которая связана с реактивным сопротивлением.

Основные современные потребители электроэнергии (асинхронные двигатели, трансформаторы, сварочные аппараты, индукционные печи) имеют активно-индуктивный характер. Уменьшить реактивное сопротивление, не изменяя параметры схемы потребителя, позволяет режим резонанса токов. Он наблюдается при параллельном соединении, которое обеспечивает независимую работу приемников.

Параллельно нагрузке подключают батарею конденсаторов (рис. 9.5), параметры которой подбирают таким образом, чтобы выполнялось условие резонанса токов: B_L = B_C .

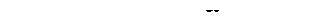В этом случае цепь имеет чисто активный характер, угол ϕ→0, cosϕ→1.

ЛЕКЦИЯ 10

ТРЕХФАЗНЫЕ ЦЕПИ

План лекции

1. Достоинства трехфазных цепей

2. Трехфазный генератор

3. Классификация и способы включения в трехфазную цепь приемни-

ков

1. Достоинства трехфазных цепей:

- наличие вращающегося магнитного поля, на основе которого построен

асинхронный двигатель;

- при передаче энергии на расстояние в трехфазных цепях по сравнению с однофазными достигается существенная экономия материала проводов;

- возможность иметь два эксплуатационных напряжения.

Трехфазные цепи – это частный случай многофазных систем. Многофазной системой называют совокупность электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся одна от другой по фазе и индуктируемые в одном источнике питания.

Каждую из цепей, входящих в многофазную систему, называют фазой.

Трехфазная цепь состоит из трех основных элементов: генератора, ли-

нии передачи и приемника.

2. Трехфазный генератор

1. Принцип действия и разметка зажимов фаз обмотки.

Простейший трехфазный генератор состоит из неподвижной (статор) и

ЭДС в неподвижных обмотках статора индуцируются в результате пересечения их витков магнитным полем, создаваемым током обмотки возбуждения вращающегося ротора (на рис. 10.1 ротор условно изображен в виде постоянного магнита), что используется на практике при относительно небольших мощностях. При вращении ротора с равномерной скоростью в обмотках фаз статора индуцируются периодически изменяющиеся синусоидальные ЭДС одинаковой частоты и амплитуды, но отличающиеся вследствие пространственного сдвига друг от друга по фазе на 2π/3 рад. (см. рис. 10.2).

Условное изображение фаз обмоток генератора и их разметка представлены на рис. 10.3. Начала обмоток принято обозначать заглавными буквами А,В,С, а концы - соответственно X ,Y, Z.

Для рассмотрения важнейшего свойства уравновешенности трехфазной системы введем понятие симметрии многофазной системы.

Система ЭДС (напряжений, токов и т.д.) называется симметричной, если она состоит из m одинаковых по модулю векторов ЭДС (напряжений, токов и т.д.), сдвинутых по фазе друг относительно друга на одинаковый угол,

2. Способы изображения симметричной системы ЭДС.

Графический

Симметричная система ЭДС – это три синусоиды, сдвинутые относительно друг друга на угол 120°. Принято считать, что начальная фаза ЭДС фазы А равна нулю, ЭДС фазы В отстает от ЭДС фазы А на 120° , ЭДС фазы С отстает от ЭДС фазы В на 120° (АВС – прямой порядок чередования фаз, АСВ – обратный порядок чередования фаз).

Тригонометрический

ЭДС можно записать как синусоидальные функции времени следующим образом:

e_A = E_m sin ωt ; e_B = E_m sin(ωt -120°) ; e_С = E_m sin(ωt +120°).

Вращающимися векторами в декартовой системе координат.

Комплексными числами.

При изображении векторной диаграммы на комплексной плоскости (рис. 10.4) каждому вектору можно сопоставить комплексное число. При расчете трехфазных цепей комплексную плоскость обычно поворачивают на

угол π/2 против часовой стрелки.

Ẻ_A =E; Ẻ_B 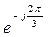= E =E 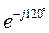=a² E,

Ẻ_C 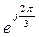= E 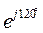=E = E 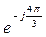= a E,

где a = e ^j120° – оператор поворота, a² = e ^j240° = e^{− j120°} .ТРЕХФАЗНЫЕ ЦЕПИ

Значение

1+ a + a² = 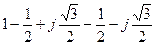= 0.

Сумма комплексных значений ЭДС трех фаз равна нулю:

Ẻ_A +Ẻ_B + Ẻ_C = E + Ee^{− j120}° + Ee^{+ j120°} = E − .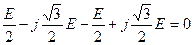

Способы соединения фаз обмоток генератора.

Соединение звездой.

Получается при объединении концов фаз обмоток X, Y, Z в нейтральную точку N (рис. 10.5).

От начал фаз к приемнику отходят линейные провода, от нейтральной

точки – нейтральный провод.

Это четырехпроводная система. Если нейтрального провода нет, получится трехпроводная система, обозначение которой Y.

 

Соединение треугольником.

 

Получается при соединении начала одной фазы с концом другой Условное обозначение: Δ .

Условные положительные направления фазных и линейных напря-

жений и соотношения между ними.

Обычно обмотки генератора соединяют звездой. Напряжения между началом и концом фазы (см. рис. 10.5) называют фазными (u_А , u_В и u_C ), а напряжения между началами фаз генератора – линейными (u_АВ , u_ВС , u_CА).

Внутренним сопротивлением фаз генератора можно пренебречь. В этом случае фазные напряжения u_А , u_В и u_C считают численно равными ЭДС фаз.

Стрелка источника показывает направление повышения потенциала. Поэтому за условные положительные направления фазных напряжений принимают направления от начала к концу фаз обмоток, а линейных напряжений – к началу фазы, являющейся вторым индексом в обозначении напряжения.

Любое линейное напряжение можно определить, рассчитав изменение потенциалов между соответствующими началами фаз генератора.

Для комплексных значений эти уравнения имеют вид:

Ů_AB = Ů_A − Ů_B ,

Ů_BC = Ů_B − Ů_C ,

Ů_CA = Ů_C − Ů_A .

Эти уравнения дают возможность построить топографическую диаграмму фазных и линейных напряжений (рис. 10.7). Следует обратить внимание на противоположное направление стрелок на схеме, указывающих условное положительное направление напряжений и соответствующих им векторов на топографической диаграмме.

Из диаграммы видно, что векторы линейных напряжений Ů_AB ,Ů_BC , Ů_CA опережают по фазе соответственно векторы фазных напряжений Ů_A ,Ů_B , Ů_C на угол 30° .

Линейное напряжение по величине больше фазного в 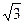раз, т. е.

U_л = 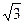U_ф или U_ф = .

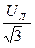При соединении фаз обмоток генератора треугольником конец одной фазы соединяют с началом другой (рис. 10.7). В этом случае линейные напряжения равны фазным: U_л =U_ф.

3. Классификация и способы включения в трехфазную цепь приемников

Трехфазные цепи бывают четырехпроводные и трехпроводные. Фазы

генератора и фазы приемника могут быть соединены по-разному.

Приемники, включаемые в трехфазную цепь, могут быть одофазными и трехфазными. Начала и концы фаз трехфазных приемников обозначают соответственно буквами а, х; b, y; с, z.

Трехфазные приемники могут быть симметричными и несимметричными. У симметричных приемников равны между собой комплексные сопротивления фаз: Ż _a = Ż _b = Ż _c .

У несимметричного приемника нагрузка может быть равномерной, если сопротивления фаз равны между собой по величине (по модулю), или однородной, если ϕ_a = ϕ_b = ϕ_c .