ЛЕКЦИЯ 11

РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ

План лекции

1. Соединение фаз приемника треугольником

2. Соединение фаз приемника звездой трехпроводной

3.Соединение звездой четырехпроводной с нейтральным проводом без

сопротивления

4. Мощности трехфазных цепей

5Способы измерения активной мощности

1. Соединение фаз приемника треугольником

Приемник несимметричный.

Для схемы замещения электрической цепи, приведенной на рис. 11.1,

Необходимо вычислить токи, если известны напряжения генератора и сопротивления фаз приемника.

В трехфазной цепи различают токи фазные (I_ab, I_bc , I_ca) и линейные токи

I _A, I_В, I_C . Фазные токи вычисляют на основании закона Ома по формулам

Ỉ_ab =Ů_ab /Ż_ab , Ỉ_bc =Ů_bc /Ż_bc , Ỉ_ca =Ů_ca /Ż_ca ,

где Ů_ab , Ů_bc и Ů_ca – комплексы напряжений на фазах приемника, а

Ż_ab, Ż_bc, Ż_ca – комплексные сопротивления фаз.

При соединении фаз приемника треугольником напряжения на его фазах равны линейным напряжениям генератора (рис. 11.1), поэтому

Ỉ_ab =Ů_AB /Ż_ab , Ỉ_bc =Ů_BC /Ż_bc , Ỉ_ca =Ů_cCA/Ż_ca .

Сопротивлением линейных проводов при этом пренебрегают.

Затем вычисляют линейные токи по уравнениям, составленным на ос-

новании первого закона Кирхгофа для узлов а, b, с:

Ỉ_A =Ỉ_ab– Ỉ_ca , Ỉ_B =Ỉ_bc– Ỉ_ab , Ỉ_C =Ỉ_ca– Ỉ_bc .

Из этих уравнений следует, что геометрическая сумма векторов линейных токов равна нулю Ỉ_A + Ỉ_B + Ỉ_C = 0 .

Приемник симметричный.

У симметричного приемника комплексные сопротивления фаз равны

между собой: Ż_ab = Ż_bc = Ż_ca . Поэтому токи в фазах равны между собой по

величине и сдвинуты относительно друг друга по фазе на 120º (2π/3) . Поэтому достаточно вычислить по закону Ома ток только одной фазы. Комплексы линейных токов определяют как разности комплексов соответствующих фазных токов.

Линейные токи по величине равны между собой и сдвинуты относительно друг друга по фазе на угол 120° . Линейный ток по величине в 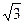раз превышает фазный: I_л = 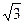I_ф .

2. Соединение фаз приемника звездой трехпроводной.

Приемник несимметричный.

Схема замещения анализируемой цепи представлена на рис.11.2.

Трехфазные цепи являются разновидностью цепей синусоидального тока, поэтому для их расчета пригодны все методы, применяемые в однофазных цепях. Анализируемую схему можно рассматривать как схему с двумя узлами (N и n) и рассчитывать токи в ней методом напряжения между двумя узлами.

Напряжение между нейтральными точками генератора и приемника можно вычислить по формуле:

Ů_nN =(Ỷ_a Ů_A + Ỷ_b Ů_B+ Ỷ_c Ů_C )/( Ỷ_a + Ỷ_b + Ỷ_c ),

Где Ỷ_a = 1/Ż_a , Ỷ_b = 1/Ż_b , Ỷ_c = 1/Ż_c – комплексные проводимости фаз приемника.

Линейные и равные им соответственно фазные токи можно определить

по закону Ома для активной ветви:

Ỉ_A=Ỉ_a=Ỷ_a(Ů_A–Ů_nN), Ỉ_B=Ỉ_b=Ỷ_b(Ů_B–Ů_nN), Ỉ_C=Ỉ_c=Ỷ_c(Ů_C–Ů_nN).

Выражения в скобках являются разностью потенциалов между началами (a,b,c) и концами (n) фаз приемников, то есть фазными напряжениями приемника. Например, Ů_a = −Ů_nN +Ů_A .

Поэтому уравнения можно переписать в следующем виде:

Ỉ_A =Ỉ_a =Ỷ_a Ů_a, Ỉ_B =Ỉ_b =Ỷ_b Ů_b, Ỉ_C =Ỉ_c =Ỷ_c Ů_c.

На основании первого закона Кирхгофа геометрическая сумма токов

Ỉ_a , Ỉ_b , Ỉ_c будет равна нулю, что дает возможность проверить правильность

решения.

Приемник симметричный.

Если приемник симметричный (Ż_a = Ż_b = Ż_c =Ż, Ỷ_a = Ỷ_b = Ỷ_c = Ỷ), то формула напряжения между двумя узлами может быть записана в виде

Ů_nN = Ỷ(Ẻ_A + Ẻ_B + Ẻ_C )/3Ỷ= 0.

Напряжение между нейтральными точками генератора и приемника не возникает.

Напряжения генератора и приемника соответственно равны. Линейные и фазные токи равны по величине и сдвинуты по фазе относительно друг друга на угол 120° :

Ỉ_A =Ỉ_a =Ů_A /Ż_a , Ỉ_B = Ỉ_a e⁻^j¹²⁰^°, Ỉ_C = Ỉ_a e ^j¹²⁰^°.

3. Соединение звездой четырехпроводной с нейтральным проводом без

сопротивления.

Схема замещения анализируемой цепи приведена на рис. 11.3

По известным значениям напряжения генератора и сопротивлений фаз приемника нужно вычислить фазные и линейные токи, а также ток в нейтральном проводе, соединяющем нейтральные точки генератора и приемника.

Приемник несимметричный.

Из схемы видно, что при соединении фаз приемника звездой, фазные и

линейные токи соответственно равны между собой, например Ỉ_А = IỈ_a .

Нейтральный провод с нулевым сопротивлением соединяет нейтральные точки генератора и приемника, следовательно, их потенциалы равны между собой: V_N =V_n

Если сопротивлением линии пренебречь, то потенциалы начал фаз генератора и приёмника одинаковы: V_A =V_a; V_B =V_b; V_C =V_c . Поэтому фазные напряжения генератора и приёмника соответственно равны: Ů_A =Ů_a , Ů_B =Ů_b ,Ů_C =Ů_c

Линейные и фазные токи определяют по закону Ома:

Ỉ_A = Ỉ_a =Ů_A /Ż_a ; Ỉ_B = Ỉ_b=Ů_B /Ż_b ; Ỉ_C= Ỉ_c =Ů_C /Ż_c .

Ток в нейтральном проводе Ỉ_nN = Ỉ_a + Ỉ_b + Ỉ_c зависит не только от характера и величины сопротивлений фаз, но и от схемы их включения. При перемене местами нагрузок двух фаз ток нейтрального провода может измениться в несколько раз.

3 Приемник симметричный.

Если приемник симметричный, токи в фазах и линиях равны между собой по величине и сдвинуты относительно друг друга по фазе на 120° . Достаточно вычислить только один ток:

Ỉ_A = Ỉ_a =Ů_A /Ż_a_.Тогда Ỉ_B = Ỉ_b = Ỉ_a e ^–^j¹²⁰^°=a²Ỉ_a : Ỉ_C = Ỉ_c = Ỉ_a e ^j¹²⁰^°=aỈ_a .

Ток в нейтральном проводе Ỉ_nN = Ỉ_a + Ỉ_b + Ỉ_c = 0.

4. Мощности трехфазных цепей.

В трехфазных цепях различают те же мощности, что и в однофазных:

мгновенную р, активную Р, реактивную Q и полную S .

Мощности р, Р и Q находят как суммы мощностей трех фаз: р = Σ р_ф ;

Р = ΣР_ф ; Q = ΣQ_ф .

Мощности каждой фазы вычисляют по известным формулам.

Потребляемой является активная мощность. Активную мощность фазы

проще всего определить по формуле Р_ф =U_ф I_ф cosϕ_ф или Р_ф = R_ф I²_ф .

Реактивную мощность фазы ищут следующим образом:

Q_ф =U_ф I_ф sinϕ_ф или Q_ф = Х_ф I²_ф .

Полную мощность трехфазной цепи вычисляют как гипотенузу сум-

марного треугольника мощностей:

S = .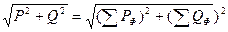

При симметричной нагрузке мощности фаз одинаковы, поэтому

P = 3P_ф = 3U_ф I_ф cosϕ_ф ; Q = 3Q_ф = 3U_ф I_ф sin ϕ_ф .

При соединении звездой U_Ф=U_Л / 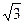и I_ф = I_Л , а при соединении треугольником U_ф =U_Л и I_Ф= I_Л/ .

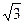Поэтому независимо от схемы соединения фаз приемника можно получить одинаковые формулы мощностей, вычисленных через линейные напряжения и токи:

Р = 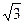U_Л I_Л cosϕ_ф ; Q = 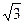U_Л I_Л sin_ϕ ;

S = 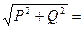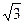U_Л I_Л .

5. Способы измерения активной мощности.

Для измерения активной мощности используют ваттметры. Числоваттметров и способ их включения зависят от способа соединения фаз приемника и от их параметров.

Ваттметр показывает активную мощность, которую вычисляют по формуле:

P_W=U_WI_Wcos [Ů_W^{^}Ỉ_W] или P_W=Re(S_W)=Re [Ů_WI^*_W],

где U_W и I_W – действующие значения напряжения и тока на ваттметре .

Угол сдвига фаз между ними соответствует одинаковым положительным направлениям Ů_W и Ỉ_W относительно зажимов, отмеченных звездочками.

Количество и способ включения ваттметров зависят от нагрузки и характеристики цепи.

Способ одного ваттметра.

Применяют при симметричной нагрузке. Ваттметр подключают такимобразом, чтобы он измерял фазные напряжение и ток (рис. 11.3, а и б). Чтобы

найти потребляемую трехфазным приемником мощность, показание ваттмет-

ра утраивают.

*

Ż

Ż

Ż

*

Часто фаза приемника недоступна. В четырехпроводной цепи ваттметр

можно подключить так, как показано на рис. 11.4, потому что линейные и

фазные токи соответственно одинаковы.

Способ двух ваттметров.

Применяют в трехпроводной цепи при несимметричной нагрузке. Схема

подключения ваттметров приведена на рис. 11.5. Сумма показаний ваттметров равна потребляемой цепью мощности. Проще это можно доказать для

комплексной мощности. Активная мощность является действительной со-

ставляющей комплексной мощности.

Комплексная мощность:

S = S_W1+ S_W2= Ů_ABI^*_A+ Ů_CBI^*_C=( Ů_A– Ů_B) I^*_A+( Ů_C– Ů_B) I^*_C=

= Ů_A I^*_A+ Ů_B[–I^*_A– I^*_C] + Ů_C I^*_C.

По первому закону Кирхгофа Ỉ_A + Ỉ_B + Ỉ_C = 0 , следовательно

I^*_A+ I^*_B+ I^*_C= 0. Отсюда I^*_B= –I^*_A– I^*_C.

Тогда S = S_W1+ S_W2= Ů_A I^*_A+ Ů_B I^*_B+ Ů_C I^*_C= S_A+ S_B+ S_C.

ЛЕКЦИЯ 12

КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ

План лекции

1. Основные понятия. Законы коммутации

2. Классический метод расчета переходных процессов

3. Подключение реального конденсатора к источнику постоянного на-

пряжения

4. Определение длительности переходного процесса

1. Основные понятия. Законы коммутации

В повседневной жизни мы постоянно наблюдаем явления, которые показывают, что не во всех электрических цепях возможно мгновенное изменение режима работы. Например, телевизор или радиоприемник продолжают некоторое время работать после отключения от источника энергии.

В цепях с реактивными элементами невозможно мгновенное изменение режима работы. Если в электрической цепи есть конденсаторы и индуктивные катушки, то при переходе от одного установившегося режима к другому наблюдается переходный процесс. Сам процесс изменения режима работы цепи (включение или выключение рубильника) в электротехнике называют комутацией.

Последовательность событий такова: установившийся режим → ком-

мутация → переходный процесс → новый установившийся режим.

Переходные процессы подчиняются двум законам коммутации.

Первый закон коммутации: ток в ветви с индуктивной катушкой не может измениться скачком.

Принято считать, что коммутация происходит мгновенно за время t = 0. Поэтому при рассмотрении переходных процессов различают два нулевых момента времени: t = 0 −, когда коммутация еще не произошла, и t = 0 + после коммутации.

Тогда первый закон коммутации можно сформулировать следующим образом: ток в индуктивной катушке до коммутации равен току в момент, наступивший сразу после коммутации, т. е. i_L (0−) = i_L (0+) .

Второй закон коммутации: напряжение на конденсаторе не может измениться скачком. Либо: u_С (0−) = u_С (0+) .

Можно дать энергетическое обоснование законов коммутации. Энер-

гию магнитного поля индуктивной катушки определяют по формуле

W_M =Li²_L /2. Мощность P_M=dW_M/dt.

Если ток i_L изменится скачком, то и W_M изменится скачком. Тогда мощность магнитного поля катушки будет равна бесконечности, что невозможно, так как не существуют реальные источники энергии с бесконечно большой мощностью.

Энергия электрического поля конденсатора W_Э = Cu²_С /2, мощность

P_Э=d W_Э/dt. Если напряжение u_С изменится скачком, то W_Э изменится скач-

ком, Р_Э = ∞, что невозможно.

Можно провести доказательства исходя и на основании формул:

u_L=(Ldi_L)/dt, i_C=(Cdu_C)/dt.

Изучение переходных процессов очень важно, так как они положены в основу принципа действия некоторых устройств и аппаратов. Кроме того, во время переходного процесса могут возникать токи и напряжения большие, чем при установившемся режиме. Электрическая цепьпригодная для номинального режима работы, может выйти из строя при подключении к источнику энергии.

2. Классический метод расчета переходных процессов

Составим систему уравнений электрического состояния в дифференци-

альной форме для схемы замещения электрической цепи. Как известно из математики, решение полученной системы линейных дифференциальных неоднородных уравнений есть сумма двух слагаемых: частного решения неоднородных уравнений и общего решения однородных уравнений.

В качестве частного решения берут принужденный режим, вызываемый внешними источниками энергии. Составляющие токов и напряжений,найденные в результате частного решения неоднородных уравнений, назы-

вают принужденными: i_пр , u_пр .

Общее решение однородного уравнения характеризует процессы, происходящие в цепи при отсутствии внешних источников энергии. Эти процессы происходят за счет изменения энергии магнитного поля катушки и электрического поля конденсатора. Составляющие токов и напряжений, найденные в результате общего решения однородных уравнений, называют свободными: i_св , u_св. Свободные осталяющие стремятся к нулю.

Классический метод расчета переходных процессов заключается в отыскании закона изменения любого тока и напряжения как суммы принужденной и свободной составляющих:

i = i_пр + i_св, u = u_пр + u_св_.

Когда свободные составляющие станут равны нулю, переходный процесс закончится. Отсюда следует, что принужденный режим – это новый установившийся режим после переходного процесса.

3. Подключение реального конденсатора к источнику постоянного напряжения

Схема замещения рассматриваемой цепи приведена на рис. 12.1.

1. Составим систему уравнений электрического состояния. Так как схема одноконтурная, то можно написать только одно уравнение по второму закону Кирхгофа: Ri + u_С =U. В этом уравнении во время переходного процесса происходит изменение двух величин: тока i и напряжения на емкостном элементе u_С. Напряжение u_С подчиняется второму закону коммутации, поэтому выразим ток по закону Ома i =(Cdu_C )/dt.ЕКЦИЯ 15. КЛАССИЧЕСКИЙ МЕТОД

Тогда уравнение примет вид:

.

2.Ищем решение этого уравнения как сумму двух слагаемых: u_С = u_{С пр}+ u_{С св}.

3. Найдем u_Спр. Теоретически переходной процесс длится бесконечно долго, поэтому принужденный режим рассмотрим как новый установившийся режим при t= ∞. Так как конденсатор постоянный ток не пропускает (i_пр = 0), то Ri_пр = 0. Отсюда u_{С пр}=U.

4. Вычислим u_Ссв. Из математики известно, что свободные составляющие меняются по экспоненциальному закону: u_Ссв= Ае^р^t.

1. Определим показатель степени р, который является корнем характеристического уравнения. Запишем уравнение электрического состояния для свободной составляющей:

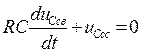
Производная 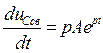. После подстановки в уравнение электрического состояния получаем

RC pAe ^pt + Ae ^pt = 0.

После сокращения на Ae ^pt: RC p + 1 = 0.

Сравнив уравнение электрического состояния с характеристическим, можно

сделать вывод: для получения характеристического уравнения, в уравнении

электрического состояния правую часть нужно приравнять к нулю, перемен-

ную величину заменить единицей, ее производную – р, вторую производ-

ную – р² и т. д.

Из решения характеристического уравнения следует, что показатель степени «е» .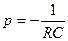

Величину 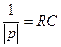обозначают τ и называют постоянной времени.

Показатель p = − 1/ τ. Так как [R]= Ом, [C] = Ф = с/Ом , то [τ]= с .

2. Определим постоянную интегрирования А.

Постоянные интегрирования определяют из начальных условий с использованием законов коммутации. Уравнение, по которому проводим решение, справедливо для любого момента времени, следовательно, и для начального:

u_С (0+) = u_{С пр}(0+) + u_{С св} (0+).

По второму закону коммутации u_С (0+) = u_С (0−) . До коммутации схема не была подключена к источнику энергии, поэтому u_С (0−) = 0.

Принужденная составляющая в данном примере является постоянной величиной, значит u_{С пр}(0+) =U.

Свободная составляющая u_Ссв = Ае^рt при t = 0+ равна А.

После подстановки получим 0 =U + A. Отсюда A = −U .

Тогда закон изменения напряжения

.

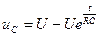Закон изменения тока можно получить либо из уравнения по второму закону Кирхгофа, либо из закона Ома.

Из уравнения по второму закону Кирхгофа:

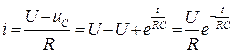
Либо .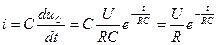

Проиллюстрируем полученные уравнения графиками (рис. 12.2, а,б).

График напряжения u_С получаем суммированием графиков u_Спр и u_Ссв. Составляющая u_{С пр}=U = const . Свободная составляющая изменяется по закону экспоненты и стремится к нулю. В начальный момент u_{С св}(0+) = −U .

График подтверждает, что напряжение на конденсаторе меняется плавно, что принужденный режим – это новый установившийся режим после переходного процесса.

График изменения тока представлен на рис. 12.2.б. При t = 0– тока не было, при t = 0+ ток i_C =U/R, далее он стремится к нулю по закону экспоненты. Графики будут меняться при изменении параметров схемы R и С. Величина напряжения от них не зависит. Величина тока обратно пропорциональна сопротивлению R и не зависит от емкости С. Длительность переходного процесса прямо пропорциональна значениям R и С.

Теоретически переходный процесс длится бесконечно долго. Практически переходный процесс заканчивается через (3–5).

Постоянная времени τ – это время, в течение которого свободные со-

ставляющие уменьшаются в е раз (e ≈ 2,7).

ЛЕКЦИЯ 13

ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЦЕПЯХ С ОДНИМ РЕАКТИВНЫМ ЭЛЕМЕНТОМ

План лекции

1. Разряд конденсатора на резистор

2. Подключение реальной катушки к источнику постоянного напряже-

ния

1. Разряд конденсатора на резистор

Схема замещения рассматриваемой цепи представлена на рис. 13.1.

В положении ключа 1 происходит уже рассмотренный процесс заряда конденсатора до напряжения источника U с постоянной времени τ_зар = R₁C.

Ток заряда конденсатора направлен от положительного зажима источника к отрицательному.

При положении ключа 2 конденсатор разряжается на резистор сопротивлением R₂. Ток i_{С раз}направлен от положительно заряженной обкладки конденсатора.

1. Составим уравнение электрического состояния цепи разряда конденсатора:

R_iС + u_С = 0. Подставив 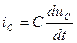, получим

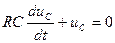. Это уравнение однородное, поэтому решение содержит только одно cлагаемое u_Ссв. Принужденная составляющая u_Спр = 0 , что очевидно, так как конденсатор разряжается.

2. Свободная составляющая меняется по закону экспоненты: u_Ссв= Ае^р^t.

Характеристическое уравнение RСp +1 = 0 . Отсюда .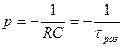

Определим постоянную интегрирования А из начальных условий с использованием законов коммутации:

u_С(0+) = u_Ссв (0+) .

Напряжение u_С (0+) = u_С (0−) =U ; u_{С св}(0+) = A. Тогда U = A.

Напряжение на конденсаторе при его разряде меняется по закону

.

Ток разряда конденсатора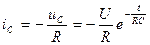

Токи заряда и разряда конденсатора направлены противоположно.

Графики изменения u_С и i_С приведены на рис. 13.2.

2. Подключение реальной катушки к источнику постоянного напряжения

Схема замещения анализируемой цепи приведена на рис. 13.3.

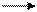
1. Уравнение электрического состояния в дифференциальной форме:

u_L + u_R =U .

После подстановки u_L и u_R , выраженных по закону Ома, получим уравнение с одной переменной:

.

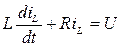2. Решение этого уравнения является суммой двух слагаемых:

i_L = i_Lпр + i_Lсв.

3. Найдем i_Lпр в схеме при t = ∞. Индуктивный элемент не оказывает сопротивления постоянному току, вместо него будет закоротка. Тогда

i_L_пр = U/R.

4. Вычислим i_Lсв по закону экспоненты: i_Lсв= Ae^pt.

Составим характеристическое уравнение для определения p: Lp + R = 0.

Отсюда p = − R / L. Постоянная времени τ = .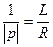

Так как [L] = Гн = с ⋅Ом, то [τ] = с.

Определим постоянную интегрирования А из начальных условий с использованием законов коммутации.

В начальный момент времени

i_L (0+) = i_L _пр (0+) + i_Lсв (0+) .

По первому закону коммутации i_L(0+) = i_L (0−) . До коммутации схема

не была подключена к источнику энергии, поэтому i_L (0−) = 0 .

Принужденная составляющая i_{L пр}=U/R – постоянная величина. Свободная составляющая в начальный момент i_Lсв (0+) = А.

После подстановки получим: 0 =(U/R) + A. Отсюда A= –U/R.

Тогда закон изменения тока:

.

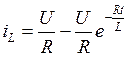Закон изменения напряжения .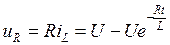

Закон изменения напряжения .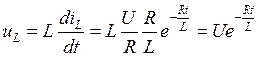

В любой момент времени u_R + u_L + .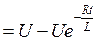

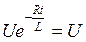Проиллюстрируем полученные законы изменения электрических вели-

чин графиками рис. 13.4 а, б.

График тока i_L получаем как сумму графиков i_Lпр и i_Lсв.

Составляющая тока i_Lпр =U/R = const. Свободная составляющая меняется по

закону экспоненты и стремится к нулю. В начальный момент

i_Lсв (0+) = −U/R.

Из графика видно, что ток в индуктивной катушке меняется плавно и

стремится к принужденной составляющей.

Графики изменения напряжений u_R и u_L приведены на рис. 13.4, б.

График u_R аналогичен графику тока i_L , так как u_R = Ri_L .

Напряжение u_L в начальный момент возрастает скачком до величины входного напряжения, а затем по экспоненциальному закону уменьшается до нуля.

<15 16 17 18 19 2021>

Дата добавления: 2015-08-20; просмотров: 1340;