ЛЕКЦИЯ 7. 1. Основные законы цепей переменного тока
АНАЛИЗ ЦЕПИ С ПОСЛЕДОВАТЕЛЬНЫМ СОЕДИНЕНИЕМ ПРИЕМНИКОВ
План лекции
1. Основные законы цепей переменного тока
2. Построение векторной диаграммы
3. Треугольники сопротивлений и мощностей
4. Резонанс напряжений
1. Основные законы цепей переменного тока
В цепях переменного тока закон Ома выполняется для всех значений,
законы Кирхгофа – только для мгновенных и комплексных, которые учиты-
вают фазные соотношения.
Первый закон Кирхгофа. Алгебраическая сумма мгновенных значений
токов в узле:
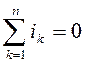, либо алгебраическая сумма комплексных значений токов в узле равна нулю:
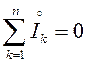
Второй закон Кирхгофа. Алгебраическая сумма мгновенных значений напряжений на приемниках в контуре равна алгебраической сумме мгновен-
ных значений ЭДС, действующих в этом же контуре:
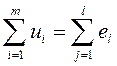, либо алгебраическая сумма комплексных значений напряжений на приемниках в контуре равна алгебраической сумме комплексных значений ЭДС в том же контуре:
.
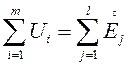Уравнения, составленные по законам Кирхгофа, называют уравнения-
ми электрического состояния.
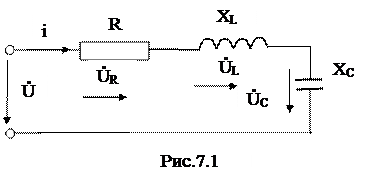Схема замещения цепи с последовательным соединением приемников представлена на рис. 7.1.
Для анализа процессов в схеме воспользуемся уравнением на основании второго закона Кирхгофа в комплексной форме:
Ů= ŮR + ŮL+ ŮC
Подставим в это уравнение значения напряжений, выраженные по закону Ома:
Ů=RỈ + jXLỈ − jXCỈ =[R + j(XL − XC )] Ỉ= Ż Ỉ,
где Ż – комплексное сопротивление цепи.
Очевидно, что Ż = R + j (X L − XC ) = R + j X ,
где R – активное сопротивление, Х – реактивное сопротивление.
Закон Ома в комплексной форме для цепи с последовательным соединением приемников: Ů = Ż Ỉ.
Реактивное сопротивление Х может быть положительным и отрицательным.
Реактивное сопротивление Х > 0, если X L > XC . В этом случае цепь имеет индуктивный характер.
Реактивное сопротивление X < 0 , если X L < XC . В этом случае цепь имеет емкостный характер.
2. Построение векторной диаграммы.
Обычно при ее построении не привязываются к комплексной плоскости, так как имеет значение только взаимное расположение векторов.
Построение векторной диаграммы начинают с вектора величины, общей для данной цепи. При последовательном соединении элементов такой величиной является ток. Вид диаграммы зависит от характера цепи. Построение векторной диаграммы для цепи, имеющей активно-индуктивный характер, т. е.
X L > XC и X > 0 , приведено на рис. 7.2.
Входное напряжение складывается из напряжений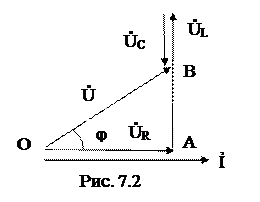 
на трех идеальных элементах при учете сдвига фаз. Напряжение на резисторе совпадает с током по фазе. Напряжение на индуктивном элементе опережает ток на 90°, на емкостном – отстает на 90° .
Полученный при построении векторной диаграммы треугольник ОАВ (рис. 7.3.) дает возможность оперировать действующими значениями, для которых законы Киргофа не выполняются:
;
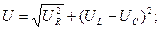
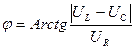
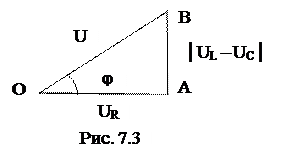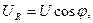
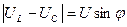
Угол φ = ψu − ψi – угол сдвига фаз тока и полного напряжения.
3. Треугольники сопротивлений и мощностей.
Если разделить все стороны треугольника напряжений на ток I, можно получить подобный ему треугольник сопротивлений (рис. 7.4), где Z – полное со-
противление цепи, R – активное сопротивление, Х – реактивное сопротивле-
ние, X L = L ⋅ω – индуктивное сопротивление, XC =1/Cω – емкостное сопротивление.
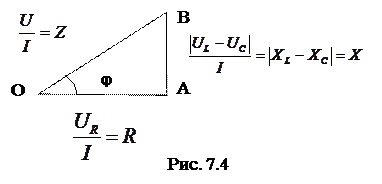
Закон Ома для действующих значений при последовательном соедине-
нии приемников имеет вид : U=Z I.НИКОВ
Из свойств треугольника сопротивлений можно получить соотношения:
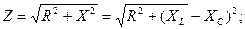
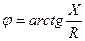; R = Z ⋅ cosϕ; X = Z ⋅ sin ϕ.
Угол ϕ зависит от соотношения сопротивлений цепи.
Сравнение формул полного и комплексного сопротивлений позволяет
сделать вывод, что полное сопротивление является модулем комплексного.
Из треугольника сопротивлений видно, что аргументом комплексного сопро-
тивления является угол ϕ. Поэтому можно записать: Z = R + jX = Z e jϕ .
Полное сопротивление любого количества последовательно соединенных приемников
Z = √ (ΣR)2 + (ΣX L − ΣXC )2 .
Умножением всех сторон треугольника напряжений на ток можно получить
треугольник мощностей (рис. 7.5).
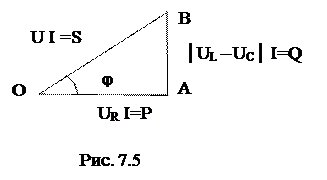
Активная мощность P =UR ⋅ I = R ⋅ I 2 =U ⋅ I ⋅ cosϕ
характеризует энергию, которая передается в одном направлении от генера-
тора к приемнику. Она связана с резистивными элементами.
Реактивная мощность Q =│ UL −UC │ ⋅ I = X ⋅ I 2 =U I sinϕ характеризует
часть энергии, непрерывно циркулирующей в цепи и не совершающей по-
лезной работы. Она связана с реактивными элементами.
Полная (кажущаяся) мощность S =U ⋅ I =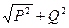 
.
Активную мощность измеряют в ваттах (Вт), реактивную – вольт-амперах реактивных (вар), полную – вольт-амперах (В⋅А ).
4. Резонанс напряжений.
Индуктивная катушка и конденсатор – взаимоподавляющие антиподы.
Когда они полностью компенсируют действие друг друга, в цепи наблюдается резонансный режим. Резонанс напряжений возникает при последовательном соединении индуктивных катушек и конденсаторов. Условие резонанса напряжений: входноереактивное сопротивление Х равно нулю.
Рассмотрим режим резонанса для цепи, схема замещения которой
представлена на рис. 7.1.
При резонансе X = X L − XC = 0. Отсюда X L = XC . Так как XL = Lω, а
XC = 1/Cω, то при резонансе Lω0 =1/Cω0 . Тогда LCω20 =1
Отсюда следует, что добиться резонанса напряжений в схеме на рис. 7.1 можно изменением индуктивности L, емкости С и частоты ω.
Циклическая резонансная частота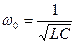 
.
Тогда частота f0 = 
.
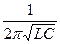При резонансе полное сопротивление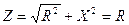 
. Цепь имеет xисто активный характер.
При резонансной частоте ω = ω0 X = 0 , X L = XC ,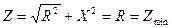 
,
I=U/R= Imax .
Цепь имеет чисто активный характер.
Значение резонанса напряжений:
1. В электроэнергетических устройствах в большинстве случаев явление нежелательное, связанное с появлением перенапряжений.
2. В электротехнике связи (радиотехнике, проволочной телефонии), в автоматике явление резонанса напряжений широко используют для настройки цепи на определенную частоту.
ЛЕКЦИЯ 8
АНАЛИЗ ЦЕПИ С ПАРАЛЛЕЛЬНЫМ СОЕДИНЕНИЕМ ПРИЕМНИКОВ
План лекции
1. Основные законы
2. Построение векторной диаграммы
3. Треугольники проводимостей и мощностей
4. Резонанс токов
1. Основные законы
Схема замещения цепи с параллельным соединением приемников изображена на рис. 8.1.
 |
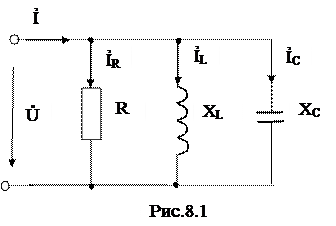Для анализа цепи применим уравнение по первому закону Киргофа для комплексных значений:
Ỉ = ỈR + ỈL + ỈC .
Далее подставим в это уравнение значения токов, выраженных по закону
Ома:
.
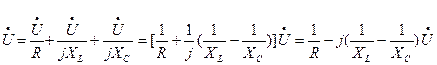Введем обозначения: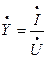 
– комплексная проводимость; 
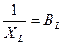индуктивная проводимость индуктивного элемента;
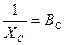– емкостная проводимость емкостного элемента;
1/R=G – активная проводимость резистивного элемента.ЛЕКЦИЯ 8. АНА
Используя введенные обозначения, можно записать:
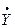= G − j (BL − BC ) = G − j B,
где В – реактивная проводимость.
2. Построение векторной диаграммы
Построение векторной диаграммы начинаем с вектора напряжения, которое является одинаковым для всех элементов схемы. Векторная диаграмма для
случая, когда X L < XC , приведена на рис. 8.2.
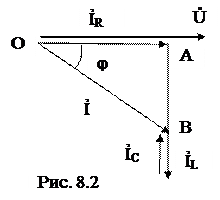Ток в неразветвленной части схемы складывается из токов трех параллельных ветвей при учете сдвига фаз. Ток через резистор совпадает с напряжением по фазе, через индуктивный элемент отстает от напряженияна на 90°, ток через конденсатор опережает его на 90° .
На основе векторной диаграммы можно изобразить треугольник токов ОАВ (рис. 8.3.)
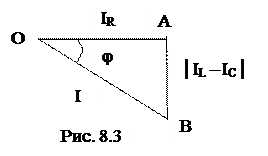
Из свойств треугольника токов получаем следующие соотношения, позволяющие оперировать действующими значениями:
;
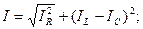
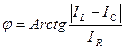IR = I cosϕ ;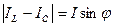 
.
3. Треугольники проводимостей и мощностей
Разделив все стороны треугольника токов на напряжение, получим подобный
ему треугольник проводимостей (рис. 8.4), где Y – полная проводимость.
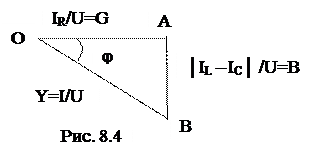
Закон Ома для действующих значений при параллельном соединении имеет вид: I = YU .
Из свойств треугольника проводимостей можно получить соотношения:
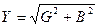; G = Y cos ϕ ; B = Y sin ϕ; ϕ = arc tg B/G .
Полная проводимость Y является модулем комплексной проводимости :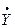
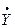= Y e- jϕ = G − jB .
Полная проводимость любого количества параллельно соединенных приемников
.
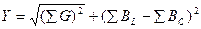Умножив все стороны треугольника токов на напряжение, можно получить
треугольник мощностей (рис. 8.5 а).
 |
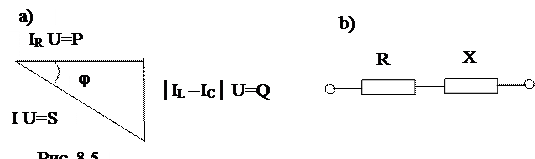Получим соотношения для активной и реактивной проводимостей ветви. Все
резистивные элементы ветви можно заменить одним эквивалентным сопро-
тивлением. Все реактивные элементы также можно заменить одним эквива-
лентным, индуктивным или емкостным. Схема замещения любой ветви в общем виде приведена на рис. 8.5 b.
Комплексная проводимость – это величина, обратная комплексному сопротивлению: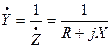 
.
Чтобы избавиться от мнимости в знаменателе, домножим числитель и знаменатель на сопряженный знаменателю комплекс:
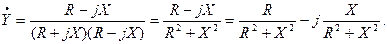
Выражение в знаменателе R2 + X 2 = Z 2 .
Тогда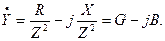 
Дата добавления: 2015-08-20; просмотров: 5134;