Точкой - сферическое движение НМС

Определение: Движение НМС, при котором одна ее точка остается неподвижной, называется движением НМС с одной неподвижной точкой или сферическим движением НМС.

Для того, чтобы найти параметры, определяющие положение НМС, т.е. обобщенные координаты, введем декартовы системы координат: неподвижную 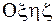и подвижную Охуz с началом в неподвижной точке О .

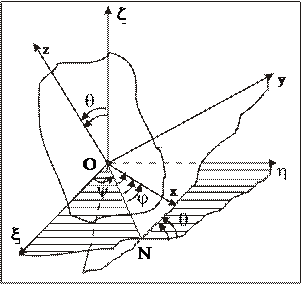
Рис. 53

Подвижная система координат Охуz неизменно связана с НМС. Плоскость Оху пересекает плоскость 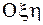по линии ОN, называемой линией узлов.

Положение подвижной системы координат относительно неподвижной определяет положение НМС в соответствующий момент времени.

Это положение определяется тремя углами: 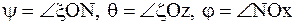, которые называются углами Эйлера.

Угол y, называемый углом прецессии, определяет положение линии узлов ОN относительно неподвижной координатной оси 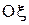. Его изменение характеризует вращение НМС с угловой скоростью 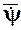относительно неподвижной координатной оси 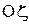, называемой осью прецессии (рис. 54).

Угол q, называемый углом нутации, определяет положение подвижной плоскости Оху относительно неподвижной плоскости 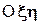(положение подвижной оси Оz относительно неподвижной оси Оz). Его изменение характеризует вращение НМС с угловой скоростью 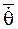относительно линии узлов ОN, называемой также осью нутации (рис. 55).

Угол j, называемый углом собственного вращения, определяет положение подвижной координатной оси Ох относительно линии узлов ОN. Его изменение характеризует вращение НМС с угловой скоростью 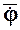относительно подвижной координатной оси Оz, называемой осью собственного вращения (рис. 56).

Следовательно, посредством трех последовательных независимых (что нетрудно доказать) поворотов НМС:

на угол y вокруг оси ,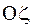

на угол q вокруг оси ОN,

на угол j вокруг оси Оz

можно НМС вместе с неизменно связанной с ней подвижной системой координат Охуz, совмещенной первоначально с неподвижной системой координат 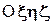, перевести в положение, которое соответствует текущему моменту времени t (рис. 56).

Таким образом, с помощью трех независимых друг от друга углов Эйлера, которые являются функциями времени и обобщенными координатами, определяется положение подвижной системы координат относительно неподвижной, а, следовательно, и положение НМС в любой момент времени.

y=y(t), q=q(t), j=j(t). (9.1)

(9.1)- уравнения движения НМС.
Эти функции, являющиеся уравнениями движения НМС, должны быть однозначными, непрерывными и дважды дифференцируемыми функциями.

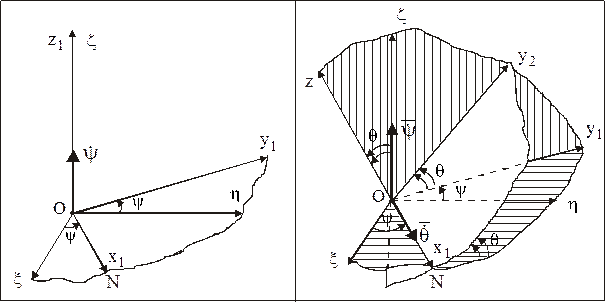
Рис. 54 Рис. 55

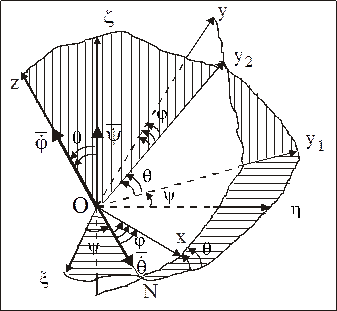
Рис. 56