Теорема о сложении ускорений МТ

Возьмем производную по времени от выражения (8.2):

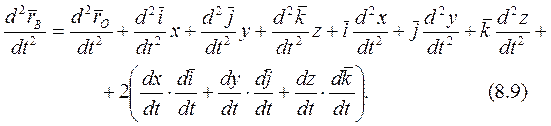
Пояснения:

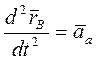, (8.10)

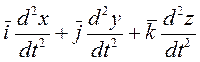, (8.11)

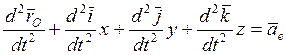, (8.12)

или 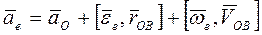. (8.13)

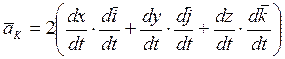. (8.14)

Подставив соотношения (8.6) в выражение (8.4), получим:

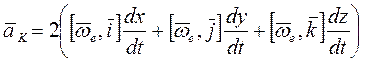или

.

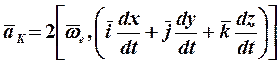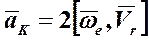. (8.15)

Ускорение 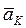называется ускорением Кориолиса или поворотным ускорением и является результатом взаимного влияния переносного и относительного движений.

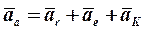. (8.16)

Теорема: Абсолютное ускорение сложного движения МТ равно геометрической сумме переносного и относительного ускорений и ускорения Кориолиса .