Сочетания с повторениями

Сочетаниями с повторениями элементов n различных типов по т называются их неупорядоченные наборы из т элементов, отличающиеся друг от друга только самими элементами.

При этом возможно т > п, поскольку допускается повторение элементов в их неупорядоченном наборе из т элементов.

Пример. Сочетания с повторениями из элементов а, b и с по 2: аb(=bа), ас(=са), bс(=сb), аа, bb, cc.

Число всех сочетаний с повторениями элементов л различных типов по неупорядоченным наборам из т элементов (обозначается 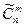) есть

= = .

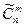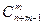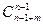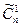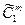Действительно, нетрудно установить начальные условия: = п, = 1. Первое условие означает, что из п различных типов элементов можно выбрать п различных сочетаний по одному элементу, причем повторений в этом случае не будет, т.е. 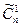= = 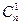п.

Второе условие означает, что из элемента одного (единственного) типа можно получить одно (единственное) сочетание из т элементов. Это будет сочетание, где элемент единственного типа повторяется т раз, т. е. 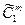= =1

Зафиксируем (обратим внимание на) элемент одного какого-то типа среди п различных типов. Тогда каждое сочетание или содержит этот тип элемента (и, следовательно, т-1остальных элементов этого сочетания можно выбрать 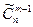способами), или нет (и, следовательно, сочетание т элементов п-1 оставшегося типа можно выбрать 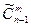способами). Используя правило суммы, получим = + .

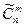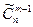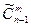Далее непосредственной проверкой убеждаемся, что если выбрать 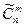= 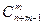(здесь 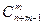- число сочетаний без повторений

из п+т-1по т или биномиальный коэффициент), то предыдущее равенство даст 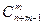= 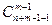+ 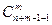или, 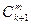= 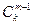+ , если обозначить k=п+т-2.

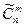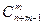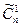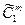Последняя формула есть основное тождество для биномиальных коэффициентов (для чисел сочетаний без повторений). Таким образом, равенство, полученное на основе правила суммы для числа сочетаний с повторениями, приводит к тождеству для биномиальных коэффициентов, если выбрать = . Можно считать последний результат угаданным, если будут выполнены начальные условия: = п, = 1.

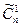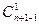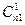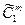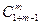При нашем выборе = = = п и = = =1.

Поскольку оба начальных условия выполнены, окончательно получаем

= = .

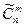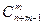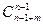Для примера сочетаний с повторениями элементов а, b, с 3 различных типов по 2 имеем

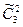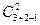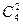= = = 4!/ (2! (4-2) !) = 6.

Решением задачи 6 является при m = 3 и п = 6

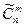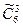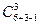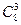= = = =8!/(3!(8-3)!)=8× 7× 6/ (1× 2 × 3) =8× 7 = 56

вариантов результатов при бросании одновременно 3 одинаковых игральных костей. Здесь п = 6 (на каждой кости возможно выпадение 6 различных типов цифр) и т = 3 (берутся сочетания цифр с возможными повторениями на 3 бросаемых костях) .