Размещения без повторений

Размещениями без повторений или просто размещениями элементов n различных типов по m называются их последовательности из m различных элементов, отличающиеся друг от друга самими элементами или их порядком. При этом m≤n, поскольку не допускается повторение элементов в последовательности из m различных элементов. (Иногда размещения называют расположениями, выборами, упорядоченными рядами или наборами, распределениями или аккомодациями.)

Пример. Размещения из 3 различных элементов а,b и с по 2: аb, bа, ас, са, bс, сb.

Число всех размещений из элементов п различных типов по т

(обозначается 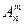) есть 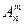= =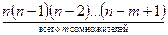n!/(n-m)!

Действительно, в последовательности из т различных элементов n возможных различных типов без повторения элемент в 1-й позиции можно выбрать любым из n типов, элемент во 2-й позиции — любым из n типов, кроме типа, встречающегося в 1-й позиции, т. е. любым из n-1 оставшихся типов. Аналогично элемент в 3-й позиции можно выбрать любым из n типов, кроме типов, встречающихся в 1-й и 2-й позициях, т. е. выбрать любым из n-2 оставшихся типов и т.д. В конце концов элемент в последней n -й позиции последовательности можно выбрать любым из n типов, кроме типов, встречающихся в n -(m-1) предыдущих позициях, т. е. любым из n-m оставшихся типов. Тогда, по правилу произведения, число последовательностей из m различных элементов n возможных различных типов без повторений или число размещений есть

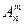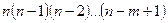= =n!/(n-m)!.

Пример. Размещение из 3 различных элементов а, b и с по 2:

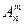= 3!/ (3-2)!=6.

Решением задачи 3 является А, = 6!/(6-3)! = 6•5•4 = 120 вариантов из 3 команд, занявших 3 первых места, в турнире из 6 команд.