Сочетания без повторений

Сочетаниями без повторений или просто сочетаниями элементов n различных типов по т называются их неупорядоченные наборы из m различных элементов, отличающиеся друг от друга только самими элементами.

При этом т < n, поскольку не допускается повторение элементов в их неупорядоченном наборе из т элементов. (Здесь и далее под неупорядоченным набором из т элементов понимается их линейно не­упорядоченное множество, аналогичное множеству разноцветных шаров, помещенных в урну, причем нет никакого порядка в их вза­имном расположении.)

Иногда сочетания называют разбиениями или композициями и даже размещениями. Последний термин неудачен, ибо он также ис­пользуется для обозначения размещений.

Пример. Сочетания из 3 элементов а, b и с по 2 : аb(=bа) , ас(=са) , bс(=сb).

Число всех сочетаний элементов п различных типов по неупорядоченным наборам из т различных элементов (обозначается 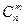) есть

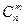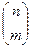= = n!/m!(n-m)!

(числа 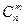часто называют биномиальными коэффициентами).

Действительно, элементы n различных типов можно разместить в последовательности из т различных элементов 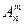=п!/(п-т)! различными способами (см. размещения без повторений) .Но при размещении без повторений в последовательности учитывается порядок взаимного расположения m различных элементов, который в сочетаниях без повторений не учитывается.

Число всех взаимных расположений m различных элементов равно числу перестановок без повторений из т различных элементов: Р_m = m! Следовательно, каждому отдельному сочетанию без повто­рений будет соответствовать m! размещений без повторений:

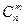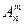= /m!, откуда 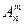= п!/((п-т)!т!).

Для примера сочетаний из 3 различных элементов а, b и с по 2 имеем:

Решением задачи 5 является 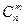= п!/(т!(п-т)!) вариантов выбора т различных предметов из п различных предметов.