А. Неупорядоченные разбиения с фиксированными размерами частей
Неупорядоченное разбиениеn -элементного множества X — это любое семейство {X1, X2,…, Xk}, где 1≤k≤п; X1, X2,…, Xk - непустые попарно непересекающиеся подмножества множества X , объединение которых равноX.
Называем такое разбиение неупорядоченным, таккак семейство — это неупорядоченнаясовокупность.
Пример.Для множества {а,b,с} неупорядоченное разбиение это, например, {{а},{b,с}}. Причем {{а},{b,с}}={{b,с},{а}}.
Для множества с п элементами обозначим через D(n; k1, k2,…, kn) число всех таких неупорядоченных разбиений,в которых есть k1 подмножеств с однимэлементом, k2 подмножеств с двумяэлементами и т.д., где k1≥0, k2≥0,…, kn≥0; k1+2 k2+…+n kn= n.
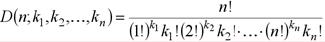Имеем
5б. Упорядоченные разбиения с фиксированными размерами частей
Упорядоченным разбиениемконечного множества X с n элементами называется любой кортеж вида <X1, X2,…, Xk>, где 1 ≤k ≤n; X1, X2,…, Xk - непустые попарно непересекающиеся, подмножества множества X, объединение которых равно X.
Называем такое разбиение упорядоченным, так как элементы кортежа упорядочены.
Пример.Для множества {а,b,с} упорядоченное разбиениеэто, например, кортеж <{{а},{b,с}}>.Причем <{{а},{b,с}}>¹<{{b,с},{а}}>.
Для множества с п элементами обозначим через E(n; m1, m2,…, mk,) число всех таких упорядоченных разбиений на подмножества X1, X2,…, Xk, содержащие m1, m2,…, mk, где m 1≥0, m 2≥0,…, m k≥0; m 1+ m 2+…+ m k= n.
Число всех упорядоченных разбиений<X1, X2,…, Xk> множества с п элементами на подмножества X1, X2,…, Xk, содержащие m1, m2,…, mk, элементов соответственно. определяется по полиномиальной формулеE(n; m1, m2,…, mk)=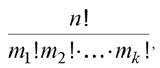
,где m 1≥0, m 2≥0,…, m k≥0; m1+ m2+…+mk= n.
2. Разбиения множества на k блоков с не фиксированными размерами частей
Определение. Упорядоченнымразбиениеммножества A на k блоков называется семейство множеств R = {A1, ..., Ak} таких, что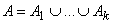 
, 
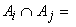
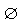для любых 
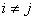и для всех i 
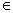{1, …, k}.
Любому разбиению множества на блоки можно взаимно однозначно сопоставить отношение эквивалентности Q, заданное на множестве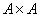 
, в котором элемент х находится в отношении Q с элементом y тогда и только тогда, когда элементы х и y принадлежат одному блоку разбиения. Поэтому задачи на разбиения часто встречаются на практике там, где возникают классы эквивалентности.
Например, отношению "2x+y делится на 3", заданному на множестве {1, ..., 10}, соответствует разбиение R = {{1, 4, 7, 10}, {2, 5, 8}, {3, 6, 9}}.
Дата добавления: 2015-08-20; просмотров: 2426;