Доказательство.
Разобьем все множество разбиений на два класса. В первый поместим разбиения, в которых последний элемент входит в отдельный блок, таких разбиений будет S(n – 1, k – 1), во второй – все остальные, т.е. те разбиения, в которых последний элемент входит в один из k непустых блоков, таких разбиений будет kS(n – 1, k).
В таблице приведены значения, вычисленные с помощью рекуррентного соотношения.
Например, S(5, 3) = S(4, 2) + 3S(4, 3) = 7 + 3*18 = 25.
Таблица значений для S(n, k )= Sп k
| Sп k | k= 1 | Суммы по каждой строке или числа Белла Bn | ||||||
| n =1 | ||||||||
В комбинаторике числом Стирлинга второго рода S(n, k) называется число неупорядоченных разбиений n-элементного множества на k непустых подмножеств.
Таблица частных значений чисел Стирлинга второго рода
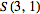
| 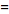
| 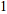
| (1) |
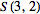
| 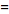
| 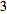
| (2) |
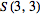
| 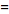
| 
| (3) |
Если множество состоит из n-элементнов, то оно имеет единственные неупорядоченные разбиения на одно и n непустых подмножеств. Поэтому имеем формулы )4).
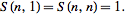
| (4) |
Таблица других свойств чисел Стирлинга второго рода
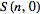
| 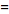
| 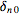
| (5) |
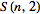
| 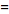
| 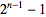
| (6) |
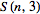
| 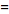
| 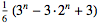
| (7) |
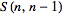
| 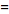
| 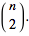
| (8) |
Таблица чисел Стирлинга второго рода
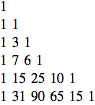
| (9) |
Более подробная таблица имеет вид (треугольник Стирлинга для числа подмножеств):
| S(n, k) | S(n, 0) | S(n, 1) | S(n, 2) | S(n, 3) | S(n, 4) | S(n, 5) | S(n, 6) | S(n, 7) | S(n, 8) | S(n, 9) |
| n =0 | ||||||||||
| n =1 | ||||||||||
Другие свойства чисел Стирлинга второго рода даны ниже.
Представление чисел Стирлинга второго рода в виде сумм с биномиальными коэффициентами 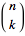 .
.
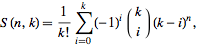
| (10) |
Производящие функции для чисел Стирлинга второго рода (здесь 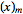 - убывающие факториалы)
- убывающие факториалы)
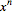
| 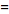
| 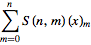
| (11) |

| 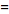
| 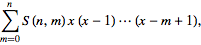
| (12) |
Экспоненциальная производящая функция для чисел Стирлинга второго рода
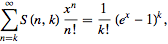
| (13) |
and
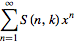
| 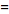
| 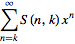
| (14) |

| 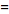
| 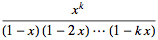
| (15) |

| 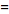
| 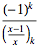
| (16) |

На рисунках выше даны диаграммы Дикау (Dickau) для наглядного представления чисел Стирлинга второго рода 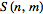 для
для 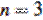 и 4. (Из источника: Dickau, R. "Visualizing Combinatorial Enumeration." Mathematica in Educ. Res. 8, 11-18, 1999)
и 4. (Из источника: Dickau, R. "Visualizing Combinatorial Enumeration." Mathematica in Educ. Res. 8, 11-18, 1999)
Рекуррентная формула для чисел Стирлинга второго рода
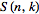
| 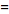
| 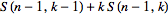
| (19) |
Для вывода некоторых из этих формул требуется более глубокие знания по математике, чем предполагается в этой лекции.
Дата добавления: 2015-08-20; просмотров: 1737;
