Сочетания с повторениями и ограничением на встречаемость элементов каждого типа

Отдельным случаем являются сочетания с повторениями элементов п различных типов по т элементов, когда элемент каждого типа должен встречаться в каждом сочетании по крайней мере (хотя бы, как минимум, не менее чем) один раз. При этом обязательно т ³n, поскольку элемент каждого из п типов встречается в каждом сочетании по т элементов не менее одного раза.

Пример. Сочетания с повторениями из элементов а, b, с по 4, когда каждый тип элементов в любое сочетание входит хотя бы один раз: ааbс, аbbс, аbсс.

Число всех сочетаний с повторениями элементов п различных типов по т элементов, когда элемент любого типа встречается хотя бы один раз в каждом сочетании (обозначается 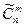(m³n):

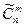(m³n)= 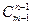, где т ³п — необходимое условие, чтобы такие сочетания существовали.

Действительно, в данном случае на сочетания с повторениями наложено дополнительное ограничение, чтобы любой из п типов элементов присутствовал в каждом наборе из т элементов хотя бы один раз. Тогда, взяв в каждом наборе из т элементов по одному элементу каждого из п различных типов, останется всего т-п элементов набора, типы которых мы можем выбирать любыми среди п различных типов элементов. Для этих оставшихся т-п элементов п возможных различных типов мы имеем обычные сочетания с повторе­ниями, т.е.

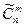(m³n)= .

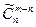Очевидно, = = = = .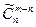

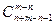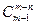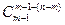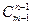Поэтому окончательно имеем 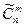(m³n)= .

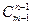Для примера сочетаний с повторениями 3 элементов а, b, с по 4, когда любой тип элементов в каждое сочетание входит хотя бы один раз, имеем 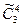(4³3)= 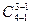= = 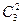3! / (2!1!) = 3 сочетания с повторениями.

Задачи на сочетания с повторениями и ограничением на встречаемость элементов каждого типа

Решением задачи 7 является 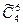(6>4) = 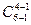= = 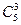5!/(3!2!) -= 5×2 = 10 вариантов подарков из 6 предметов в каждом, составленных из 4 видов предметов, если каждый вид предметов входит в каждый подарок хотя бы один раз. Основные типы комбинаторных задач, приводящие к перестановкам, размещениям и сочетаниям без повторений и с повторениями, приведены в табл. 2.1.